введение и алгоритм UCB1 / Блог компании Surfingbird / Хабр
Это первый пост из блога Surfingbird, который я выношу в общие хабы алгоритмов и искусственного интеллекта; честно говоря, раньше просто не догадался. Если интересно, заходите к нам, чтобы прочесть предыдущие тексты, – я не знаю, что произойдёт, если просто добавить новые хабы к постам несколькомесячной давности.
Краткое содержание предыдущих серий о рекомендательных системах:
В этот раз начинаем новую тему – о многоруких бандитах. Бандиты – это самая простая, но от этого только более важная постановка задачи в так называемом обучении с подкреплением…
Мы всё время говорим, что то, что мы делаем, – это машинное обучение (machine learning). Однако задумайтесь: как вы на самом деле обучаетесь? Неужели мы с вами строим регрессию движения пальцев на основе наблюдений за машинистками для того, чтобы научиться слепой печати? Неужели ребёнок, чтобы научиться ходить, сначала собирает и обобщает коллекцию примеров прямохождения родителей? На самом деле, конечно, нет: в таких случаях мы просто пробуем что-нибудь сделать, смотрим, получилось ли, а затем пытаемся (обычно бессознательно) скорректировать своё поведение на основе полученного результата.
Такая постановка задачи называется обучением с подкреплением: есть агент, который действует в какой-то среде; агент пытается что-то делать, а среда в ответ на его действия выдаёт агенту плюшки или, наоборот, бьёт током. Агент старается получить плюшек побольше, а током – пореже. В общем, типичная мышка в лабиринте.
Сегодня, однако, мы поговорим о мышке, которая попала даже не в лабиринт, а в самый обычный skinner box – давайте предположим, что состояние среды/агента от действия к действию не изменяется. Иначе говоря, у агента есть некоторый набор возможных действий, агент выбирает одно из них, получает за это некоторое вознаграждение (которое является случайной величиной), а затем снова может выбирать из тех же действий. В машинном обучении такая постановка задачи получила название многоруких бандитов (multiarmed bandits): вы сидите в комнате перед несколькими игровыми автоматами и должны постараться выиграть как можно больше.
(картинка с сайта Microsoft Research)
Зачем это нужно в реальной жизни? К примеру, представьте себе, что вы – Yahoo! или, скажем, mail. ru. У вас есть домашняя страница, на которой бывают миллионы людей каждый день. Вы хотите размещать на ней ссылки так, чтобы на них кликали как можно чаще. Как выбрать те ссылки, которые дают максимальный CTR (click-through ratio)? Здесь каждый показ ссылки пользователю соответствует «дёрганию за ручку»; каждый клик – успех, положительное подкрепление от среды; не-клик – неудача. Задача алгоритма будет в том, чтобы как можно быстрее понять, что та или иная новость «горяча», и начать её показывать (да, это чуть модифицированная задача, в которой бандиты время от времени умирают и рождаются вновь).
ru. У вас есть домашняя страница, на которой бывают миллионы людей каждый день. Вы хотите размещать на ней ссылки так, чтобы на них кликали как можно чаще. Как выбрать те ссылки, которые дают максимальный CTR (click-through ratio)? Здесь каждый показ ссылки пользователю соответствует «дёрганию за ручку»; каждый клик – успех, положительное подкрепление от среды; не-клик – неудача. Задача алгоритма будет в том, чтобы как можно быстрее понять, что та или иная новость «горяча», и начать её показывать (да, это чуть модифицированная задача, в которой бандиты время от времени умирают и рождаются вновь).
Другой пример: представьте себе, что вы хотите протестировать какой-то набор изменений в интерфейсе своего сайта. Обычно это делается при помощи так называемого A/B testing – вы должны выбрать группу для эксперимента (по каждому изменению в отдельности), контрольную группу, для которой ничего не изменится, затем собрать статистику и оценить, значимо ли улучшение. Однако такая схема сама по себе не отвечает на главный вопрос – как долго надо собирать статистику? Здесь бандиты тоже могут придти на помощь, постановка задачи ведь в точности бандитская: показ того или иного варианта соответствует дёрганию за ручку, а действия пользователя определяют ответ окружающей среды (см. , например, вот этот пост).
, например, вот этот пост).
Однако вернёмся к постановке задачи. На первый взгляд кажется, что задача выбрать оптимальную ручку очень простая: нужно дёрнуть за каждую ручку по тысяче раз, а потом выбрать ручку с наибольшим средним. И действительно, такой алгоритм, скорее всего, сделает правильный выбор – но сколько он потеряет «денег» на субоптимальных ручках! Многих из этих потерь можно было бы избежать. Вообще, лучшая метрика для оценки качества «бандитского» алгоритма – это его потери (regret) по сравнению с оптимальным алгоритмом, т.е. ожидание разности дохода от стратегии «всегда дёргать за оптимальную ручку» и рассматриваемой стратегии.
В качестве примера я сразу приведу алгоритм с одними из самых лучших гарантий на эту самую меру потерь на обучение. Это алгоритм UCB1; сам алгоритм очень простой, доказательство его оптимальности, конечно, не такое простое, но в это мы углубляться не будем, а интересующихся я отсылаю к статье [Auer et al., 2002]; там же можно найти и более «продвинутую» версию с улучшенными константами.
- Инициализация: дёрнуть за каждую ручку один раз.
- Пока продолжается работа:
- дёрнуть за ручку j, для которой максимальна величина
,
где – средний доход от ручки j, nj – то, сколько раз мы дёрнули за ручку j, а n – то, сколько раз мы дёргали за все ручки.
- дёрнуть за ручку j, для которой максимальна величина
Хотя формальное доказательство того, что здесь должно быть именно два натуральных логарифма, а не что-то другое, выходит за пределы этой статьи, интуитивно совершенно понятно, что происходит в этом алгоритме: мы придумали эвристику, оценку приоритета, по которой мы выбираем, за какую ручку дёргать. Логично, что этот приоритет тем больше, чем больше средний доход, но не только: бонус также получают те ручки, за которые мы дёргали редко (по сравнению с другими ручками). Поскольку числитель дроби растёт гораздо медленнее, чем знаменатель, при эвристика становится всё больше похожа на простой выбор ручки с оптимальным средним. Однако если какой-то из ni совсем перестанет расти (мы совсем разочаруемся в одной из ручек), рано или поздно даже логарифмический числитель заставит нас её ещё раз перепроверить.
Реализация этого алгоритма на вашем любимом языке, понятное дело, никаких трудностей не представляет – нужно просто запоминать, сколько раз дёргали за каждую ручку. Главный пафос здесь в том, что хорошо работает такая простая эвристика: можно просто выбирать ручку с максимальным приоритетом и больше ни на что не обращать внимания. Это связано с так называемой теоремой Гиттинса: оказывается, что в достаточно общих предположениях выбор оптимальной стратегии в задаче о многоруких бандитах сводится к подсчёту независимых приоритетов для каждой ручки в отдельности. Правда, теорема Гиттинса сама по себе даёт только крайне сложный и медленный алгоритм вычисления этих приоритетов (так называемых индексов Гиттинса), и алгоритм UCB – это не просто частный случай общей теоремы, а отдельный результат.
В следующей серии мы продолжим рассматривать «бандитские» задачи и обобщим их до задач следования за трендами, когда доходы разных «ручек» могут изменяться во времени, и наша задача – быстро понимать, что и где изменилось.
Алгоритм действий при присасывании клеща
Памятка по профилактике клещевых инфекций
Обращаем внимание жителей и гостей Республики Алтай о необходимости принятия мер по профилактике присасывания клещей. Клещи распространены на всей территории Республики Алтай: в прошедшем 2020 году зарегистрированы случаи присасывания переносчиков во всех населенных пунктах региона, включая город Горно-Алтайск.
Помните, самый лучший способ защититься от клещевых инфекций – не допустить присасывания клеща. Для этого, необходимо осматривать себя и своих близких ежедневно. При посещении парков, скверов, леса, сада, кладбищ одежда не должна допускать заползания клещей и, по возможности, не затруднять быстрый осмотр для их обнаружения. Пользуйтесь аэрозолями с пометкой «против клещей» «Пикник», «Гардекс», «ДЭТА» (средства «от комаров и клещей» менее эффективные).
Застрахуйтесь на случай присасывания клеща, так как при наличии страховки иммуноголобулин против клещевого энцефалита вводится бесплатно и бесплатно проводится исследование клеща на вирус клещевого энцефалита.
В случае присасывания клеща необходимо принять срочные меры.
Алгоритм действий при присасывании клеща
Присосавшегося клеща надо удалить либо в домашних условиях, либо обратившись в медицинское учреждение.
Если удаляете клеща дома, приложите на несколько секунд к клещу ватку, смоченную нашатырным спиртом или одеколоном (но не маслом, как это обычно советуют), затем ниткой завяжите узелок вокруг впившейся части клеща. Осторожно, потягивая концы нити кверху и в стороны, вытягиваем его. Вместо нитки можно использовать пинцет («клещедёр»), которым следует захватить клеща и выкручивающим движением удалить его. Место, где клещ присосался, нужно смазать дезинфицирующим раствором. Ни в коем случае нельзя раздавливать клеща, т.к. можно втереть возбудителя в кожу и заразиться клещевым энцефалитом.
Удалённого клеща необходимо поместить во флакон с плотно притёртой крышкой (куда положить кусочек ватки, смоченной водой, чтобы клещ не высох), и доставить на исследование в серологическую лабораторию (Горно-Алтайск, проспект Коммунистический, 175) для выявления вируса клещевого энцефалита. Исследованию подлежит неповреждённый клещ (не разорванный). Если нет возможности доставить клеща на исследование, его лучше сжечь.
Исследованию подлежит неповреждённый клещ (не разорванный). Если нет возможности доставить клеща на исследование, его лучше сжечь.
Для экстренной профилактики используют человеческий иммуноглобулин против клещевого энцефалита. В Горно-Алтайске это можно сделать в приемном покое или амбулатории республиканского Центра по профилактике и борьбе со СПИД (Шоссейная, 38). В районах следует обратиться в приемный покой районной или участковой больницы, на ФАП. Препарат вводят не привитым лицам, отметившим присасывание клещей. Вакцинированным лицам препарат вводят в случае множественного присасывания клещей и лицам, застраховавшимся на случай укуса клеща. Следует помнить, что введение иммуноглобулина наиболее эффективно в течение первых суток после присасывания клещей.
В случае невозможности введения иммуноглобулина необходимо использовать антивирусные препараты «Анаферон», «Ремантадин» или «Йодантипирин» согласно инструкции по применению.
Учитывая, что в клеще одновременно с вирусом клещевого энцефалита могут находится другие возбудители (риккетсии, боррелии, эрлихии, анаплазмы), целесообразно провести профилактическую антибиотикотерапию (5-дневный курс лечения «доксициклином»).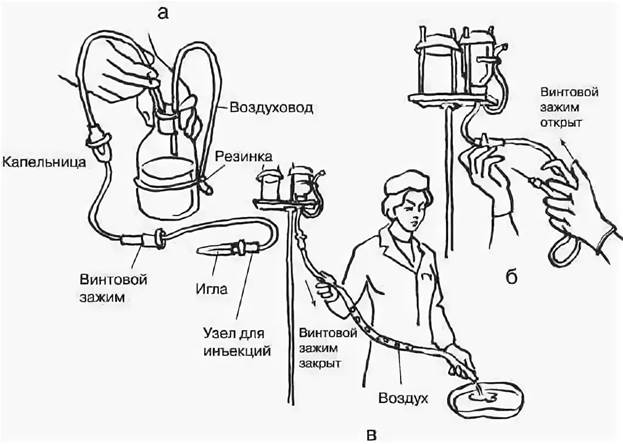
После удаления клеща и проведения экстренной серопрофилактики в течение месяца необходимо следить за состоянием здоровья и при повышении температуры или головной боли немедленно обратиться к врачу, сообщив о факте присасывания клеща.
Удаление клеща при помощи нити:
Другие способы удаления клеща:
https://ok.ru/video/11385898278
Делимобиль: после введения алгоритмов безопасности показатель аварийности снизился на 20%
ООО «Каршеринг Руссия» 01 февраля 2021 11:43
Делимобиль оценил влияние введения алгоритмов повышения безопасности на снижение аварийности. Результаты первых трех месяцев показывают существенную положительную динамику: сейчас зафиксировано снижение уровня* ДТП на 20% в сравнении с тем же периодом предыдущего года.
На снижение аварийности влияет введение рейтинга клиентов, автоматической онлайн идентификации (liveness) пользователя и смарт-тестирование при ночных бронированиях, которое оценивает скорость реакции водителя и степень концентрации внимания. В случае непрохождения digital теста система блокирует клиента на 4 часа. Таким образом, влияние комплекса всех этих мер носит позитивный накопительный характер на статистику аварийности, что особенно актуально в условиях зимнего сезона.
Наибольшее снижение аварийности произошло в Москве и Санкт-Петербурге – на 28%, далее следуют Екатеринбург — 25% и Нижний Новгород – 20%. Остальные регионы также улучшили показатели на 15-18%, некоторые из них изначально отличались высокими показателями безопасного вождения.
В первые дни введения рейтинга доля клиентов с показателем выше 4.5 (что является сверхвысоким значением в системе оценки) составила около 3%, за три месяца эта доля выросла в два раза.
В большинстве своем пользователи распределены по рейтингу равномерно от 1,5 до 4,5 баллов. А доля тех, кто находится ниже отметки 1,5 баллов продолжает уменьшаться.
Показатель рейтинга выше 3, как правило, говорит о том, что водитель уж старается соблюдать ПДД, не нарушать скоростной режим и следит за своей манерой вождения.
С введением алгоритмов безопасности также улучшилась манера вождения в категории 18/0, (водители со стажем менее года и/или возраста до 19 лет) — так, например, уровень ДТП снизился по этой группе на 10 процентных пунктов. (Снятие ограничений по стажу и возрасту коснулось только регионов, в Москве минимальный возраст для стажа менее года – 26 лет).
Бехтина Елена, CEO компании:
«Мы видим, что наши меры по снижению аварийности работают и намерены на этом не останавливаться – впереди работа над улучшением действующих алгоритмов и запуск новых. Наша цель – чтобы водители каршеринга вообще не попадали в ДТП и не были их причиной. Мы
Мы
работаем более, чем в 10 городах, и одна из наших приоритетных задач – воспитать культуру вождения среди автомобилистов».
*отношение количества ДТП по вине водителя Делимобиль на минуту в режиме вождения
Сейчас клиентская база Делимобиля составляет более 5 млн. пользователей, а в день совершается более 80 тыс. аренд.
О «Делимобиль»:
«Делимобиль» — крупнейший независимый федеральный сервис каршеринга, открытый в 2015 году. Объединив в себе весь передовой опыт каршеринга европейских стран, Делимобиль по праву стал важной и неотъемлемой частью транспортной инфраструктуры городов. Насчитывает около 15 тысяч автомобилей в Москве, Санкт-Петербурге, Самаре, Тольятти, Нижнем Новгороде, Екатеринбурге, Новосибирске, Краснодаре и Туле. По данным исследования Роскачества в 2020 году, Делимобиль признан лидером по параметру «Удобство пользования» среди мобильных приложений российский каршеринговых компаний. Официальный сайт: https://delimobil.ru/
Официальный сайт: https://delimobil.ru/
Пресс-релиз подготовлен на основании материала, предоставленного организацией. Информационное агентство AK&M не несет ответственности за содержание пресс-релиза, правовые и иные последствия его опубликования.
Алгоритмы, принципы и оптимальные сроки введения адаптированных и специализированных смесей для вскармливания детей грудного возраста | #02/21
Резюме. Официальные инструкции и рекомендации по вскармливанию детей грудного возраста нередко не поспевают за появлением новых наименований и разновидностей адаптированных и специальных смесей. Грудное молоко является оптимальным продуктом для вскармливания детей первых месяцев жизни, оно содержит многочисленные стимулирующие факторы, обеспечивающие развитие иммунной и пищеварительной систем, формирование нормального биоценоза. Естественное вскармливание способствует дозреванию этих систем и формирует наиболее физиологичный путь дальнейшего функционирования. Однако, если материнского молока недостаточно для обеспечения адекватного вскармливания или по каким-то причинам естественное вскармливание невозможно, возникает вопрос о введении докорма. В понятие «докорм» включаются смеси – заменители грудного молока. В этой статье мы предлагаем алгоритм, который позволит практикующему врачу свободно ориентироваться во всем многообразии искусственных смесей не только на текущий момент, но и на будущее, когда на рынке появятся новые продукты. Понимая принципы введения смесей, изложенные в этой статье, педиатру будет достаточно легко экстраполировать эти принципы на смеси, которые появятся в будущем.
Однако, если материнского молока недостаточно для обеспечения адекватного вскармливания или по каким-то причинам естественное вскармливание невозможно, возникает вопрос о введении докорма. В понятие «докорм» включаются смеси – заменители грудного молока. В этой статье мы предлагаем алгоритм, который позволит практикующему врачу свободно ориентироваться во всем многообразии искусственных смесей не только на текущий момент, но и на будущее, когда на рынке появятся новые продукты. Понимая принципы введения смесей, изложенные в этой статье, педиатру будет достаточно легко экстраполировать эти принципы на смеси, которые появятся в будущем.
Давно изученный и доказанный факт состоит в том, что грудное молоко (ГМ) является оптимальным продуктом для вскармливания детей первых месяцев жизни. ГМ содержит многочисленные стимулирующие факторы, обеспечивающие развитие иммунной и пищеварительной систем, формирование нормального биоценоза. Таким образом, естественное вскармливание способствует дозреванию этих систем и формирует наиболее физиологичный путь их дальнейшего функционирования. Реализация этой функции ГМ обеспечивается не только уникальным набором биологически активных веществ ГМ (гормоны, антитела, иммунные комплексы), но и его химическим составом, то есть содержанием в нем белков, жиров, углеводов, витаминов и микроэлементов, находящихся в оптимальных концентрациях и соотношениях.
Реализация этой функции ГМ обеспечивается не только уникальным набором биологически активных веществ ГМ (гормоны, антитела, иммунные комплексы), но и его химическим составом, то есть содержанием в нем белков, жиров, углеводов, витаминов и микроэлементов, находящихся в оптимальных концентрациях и соотношениях.
Критерии достаточности грудного молока и адекватности естественного вскармливания
Существуют взаимосвязанные критерии достаточности ГМ (адекватности естественного вскармливания):
- Прибавка в весе ребенка составляет не менее 150 г в неделю (600 г в среднем за месяц). Должно насторожить, если ребенок прибавляет меньше 150 г в неделю 2 недели подряд.
- Интервал между кормлениями составляет не менее 1,5 часов.
- Количество употребляемого ребенком материнского молока соответствует потребности 1/5 от реального веса – до 1 месяца; 1/6-1/7 – до 5-6 месяцев. Количество высасываемого ребенком молока можно узнать, проводя контрольное взвешивание, причем не однократное, а в течение суток (и лучше нескольких суток подряд).

Если ребенок наедается и хорошо прибавляет в весе, его питание нужно признать адекватным, и до 4-5 месяцев такому грудничку не требуется менять питание (вводить докорм и прикорм). Если имеются отклонения, нужно выяснить, связаны ли они с заболеваниями или дисфункциями или же причиной является дефицит ГМ.
Если материнского молока недостаточно для обеспечения адекватного вскармливания или по каким-то причинам естественное вскармливание невозможно, возникает вопрос о введении докорма. В понятие «докорм» включаются смеси – заменители ГМ.
Логично, чтобы эти смеси были бы максимально приближены по составу и свойствам к ГМ. Смесей, полностью заменяющих материнское молоко по всем параметрам, пока не существует. Но есть максимально приближенные по химическому составу (то есть по содержанию белков, жиров, углеводов и т. д.) – это адаптированные молочные смеси на основе коровьего или козьего молока [1, 2]. В то же время существуют лечебные смеси, химический состав которых в большей или меньшей степени отличается от оптимального за счет снижения содержания основных компонентов и полного или частичного расщепления белка (гидролизации).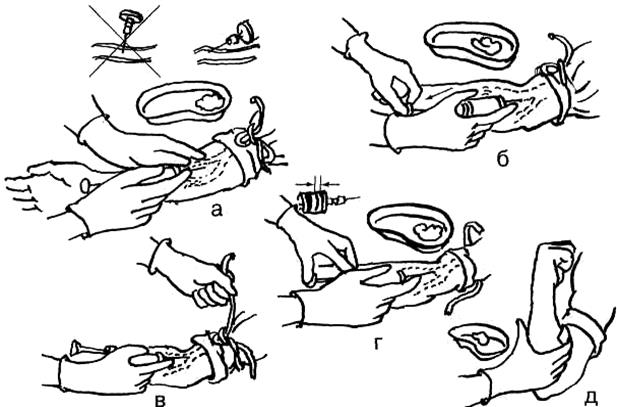
Адаптированные молочные смеси на основе коровьего и козьего молока, максимально приближенные по составу к ГМ
Адаптированные заменители в наибольшей степени приближены к женскому молоку по всем его компонентам: в них снижено по сравнению с коровьим молоком общее содержание белка (до 1,4-1,6 г/100 мл), причем белковый компонент представлен смесью казеина (основного белка коровьего молока) и белков молочной сыворотки (доминирующих в женском молоке) в соотношении 40:60 или 50:50. Это близко к их соотношению в зрелом женском молоке (45:55). Сывороточные белки образуют в желудке более нежный и мелкодисперсный сгусток, чем казеин, что обеспечивает их более высокую степень переваривания и усвоения. Примерами подобных смесей могут быть Фрисо Голд, Нан Оптипро, Нутрилон Премиум и др.
Достоинством смесей на козьем молоке являются более мелкие молекулы белка казеина, которые незрелой пищеварительной системе ребенка проще переварить. Кроме того, козье молоко богато природными олигосахаридами, их содержание в козьем молоке в 5-10 раз выше, чем в коровьем. Из 14 изученных олигосахаридов козьего молока 5 идентичны олигосахаридам ГМ [3]. Они не подвергаются разрушению при производстве смесей [4]. Козье молоко также содержит в 4-5 раз больше природных нуклеотидов, что позволяет избегать добавок их синтетических аналогов в детские смеси [5]. Примером смесей на козьем молоке являются Кабрита и др. При этом стоит отметить, что результаты клинической апробации смесей Кабрита показали общий положительный эффект на функционирование желудочно-кишечного тракта (ЖКТ) младенцев – смеси способствуют уменьшению частоты и интенсивности проявлений симптомов функциональных нарушений пищеварения у детей с минимальными проявлениями дисфункций ЖКТ, нормализуют характер стула у детей со склонностью к запорам, хорошо переносятся и подходят малышам со сниженным аппетитом [6].
Из 14 изученных олигосахаридов козьего молока 5 идентичны олигосахаридам ГМ [3]. Они не подвергаются разрушению при производстве смесей [4]. Козье молоко также содержит в 4-5 раз больше природных нуклеотидов, что позволяет избегать добавок их синтетических аналогов в детские смеси [5]. Примером смесей на козьем молоке являются Кабрита и др. При этом стоит отметить, что результаты клинической апробации смесей Кабрита показали общий положительный эффект на функционирование желудочно-кишечного тракта (ЖКТ) младенцев – смеси способствуют уменьшению частоты и интенсивности проявлений симптомов функциональных нарушений пищеварения у детей с минимальными проявлениями дисфункций ЖКТ, нормализуют характер стула у детей со склонностью к запорам, хорошо переносятся и подходят малышам со сниженным аппетитом [6].
Основным углеводом женского молока и адаптированных молочных смесей является лактоза, которая обладает рядом свойств, имеющих важное физиологическое значение для младенцев. Она способствует всасыванию кальция, обладает бифидогенным действием (т. е. способностью поддерживать рост бифидобактерий), снижает рН в толстом кишечнике. Последние два ее свойства обусловлены тем, что большая часть лактозы (до 80%) не всасывается в тонком кишечнике и поступает в толстый кишечник, где служит субстратом для B. bifidum и лактобактерий, под влиянием которых она подвергается сбраживанию с образованием молочной кислоты. Лактотрофное питание в раннем периоде жизни является основой для всех обменных процессов. Более того, лактотрофное питание – это источник веществ и стимулов, служащих непосредственно для развития и роста всех функциональных систем организма ребенка, в том числе головного мозга и центральной нервной системы.
е. способностью поддерживать рост бифидобактерий), снижает рН в толстом кишечнике. Последние два ее свойства обусловлены тем, что большая часть лактозы (до 80%) не всасывается в тонком кишечнике и поступает в толстый кишечник, где служит субстратом для B. bifidum и лактобактерий, под влиянием которых она подвергается сбраживанию с образованием молочной кислоты. Лактотрофное питание в раннем периоде жизни является основой для всех обменных процессов. Более того, лактотрофное питание – это источник веществ и стимулов, служащих непосредственно для развития и роста всех функциональных систем организма ребенка, в том числе головного мозга и центральной нервной системы.
В состав практически любой адаптированной смеси входят: сухое обезжиренное коровье (козье) молоко, деминерализованная молочная сыворотка, растительные масла, лактоза, крахмал, смесь витаминов, минеральных веществ и микроэлементов, таурин, карнитин. Все смеси делятся на ступени: первая – для детей от рождения до 6 месяцев, вторая – от 6 месяцев до 1 года, третья – от 1 года. Номер ступени обозначается соответствующей цифрой рядом с названием смеси [7].
Номер ступени обозначается соответствующей цифрой рядом с названием смеси [7].
Следует отметить, что адаптированные молочные смеси имеют натуральный вкус, максимально приближенный к таковому у ГМ, что позволяет долго сохранять смешанное вскармливание. Ингредиентный и химический составы всех современных заменителей женского молока, соответствующих международным стандартам, достаточно близки между собой. В то же время в практике нередки случаи, когда ребенок дает аллергические (псевдоаллергические) реакции на одну из современных максимально адаптированных смесей, но хорошо переносит другую того же поколения. Это указывает на необходимость максимальной индивидуализации питания детей. Критерием здесь могут служить только результаты внимательного наблюдения за ребенком в динамике и оценка переносимости им конкретного продукта, безусловно, при наличии ясных представлений врача о его ингредиентном и химическом составе [8].
Неадаптированные молочные продукты (молоко, кефир и др. ) не соответствуют физиологическим особенностям детей первого года жизни и не должны включаться в их рационы до 6-8 месяцев жизни даже в очень сложных социально-экономических условиях. Высокое содержание минеральных солей в коровьем молоке, кефире и других неадаптированных цельномолочных продуктах приводит при потреблении их детьми первых месяцев жизни к значительной нагрузке на канальцевый аппарат почек, нарушениям в водно-электролитном балансе, усилению выведения жиров в виде кальциевых солей и др.
) не соответствуют физиологическим особенностям детей первого года жизни и не должны включаться в их рационы до 6-8 месяцев жизни даже в очень сложных социально-экономических условиях. Высокое содержание минеральных солей в коровьем молоке, кефире и других неадаптированных цельномолочных продуктах приводит при потреблении их детьми первых месяцев жизни к значительной нагрузке на канальцевый аппарат почек, нарушениям в водно-электролитном балансе, усилению выведения жиров в виде кальциевых солей и др.
Специальные смеси
Если у ребенка нет проблем с пищеварением или кожных высыпаний (что тоже является проблемой ЖКТ), то при необходимости докорма ему вводится обычная молочная смесь. При проблемах с введением обычных адаптированных смесей может решаться вопрос о введении лечебных смесей. Существуют специальные смеси, в которых к обычной смеси добавляется какой-то компонент, придающий ей лечебные свойства, например, лактулоза, инулин, прочие пре- либо пробиотики, клейковина рожкового дерева.
Такие специализированные продукты обладают всеми свойствами адаптированных молочных смесей, имеют полноценный состав, не угнетают развитие собственной системы пищеварения. Имеются антирефлюксные смеси (например, Нутрилон антирефлюкс) и те, что помогают при запорах и коликах (например, Фрисовом, Семпер Бифидус).
Для недоношенных и маловесных детей (с массой тела при рождении менее 2500 г, а в особенности – менее 2000 г) применяются специальные смеси с маркировкой «пре» или «неошур». Энергетическая ценность таких смесей повышена и составляет в среднем 80 ккал на 100 мл, обычно в них больше белка, жиров и углеводов. Добавление нуклеотидов в смесь помогает стимулировать соматический рост, а также укреплять иммунную систему. Эти соединения положительно влияют на созревание кишечника и формирование микрофлоры ЖКТ. Вскармливание такими специальными смесями обычно рекомендуется до достижения веса 3000 г, затем осуществляется постепенный переход на обычную адаптированную смесь [9].
Лечебные смеси могут не содержать каких-то компонентов адаптированных обычных смесей (например, лактозы или некоторых белков). Очень широко представлена группа специальных лечебных смесей – смеси со значительными отклонениями от оптимального состава, то есть химического состава ГМ: частичные гидролизаты (гипоаллергенные смеси), полные гидролизаты, аминокислотные смеси (максимально глубокое расщеп-ление белка), смеси с пониженным содержанием лактозы или ее полным отсутствием (низколактозные и безлактозные). Эти смеси не только стоят дороже обычных, но и не в лучшую сторону отличаются от них по вкусу, что чаще всего детям не нравится, поэтому могут возникнуть проблемы с их введением [10].
К специальным смесям также относятся соевые (например, Фрисосой), назначение которых возможно при обоснованном подозрении на аллергию к белку коровьего молока. Следует отметить, что такая аллергия встречается довольно редко. Гораздо реже, чем диагноз «аллергия на белок коровьего молока». Поэтому педиатру имеет смысл критично оценивать аргументы в пользу замены молочных смесей на соевые.
Поэтому педиатру имеет смысл критично оценивать аргументы в пользу замены молочных смесей на соевые.
Кисломолочные смеси также отличаются от оптимального состава и относятся скорее к прикорму, чем к докорму. Поэтому их нежелательно вводить до 4–6 месяцев и использовать как замену ГМ [11].
Целесообразность лечебного питания детей первого года жизни
Вопрос о введении лечебного питания у детей первого года жизни возникает в основном в двух ситуациях: лактазная недостаточность (лактозная непереносимость) и пищевая аллергия (проявления дерматита) [12]. Соответственно назначаются лечебные смеси со сниженным содержанием лактозы (либо полностью безлактозные), полные или частичные гидролизаты, соевые смеси. С одной стороны, назначение лечебного питания отчасти улучшает клинические проявления, сопровождающие указанные нарушения, но, с другой, существует ряд значительных минусов, которые часто могут перечеркнуть всю потенциальную пользу и даже ухудшить состояние ребенка [13].
Во-первых, лечебное питание зачастую назначают вместо ГМ, тем самым лишая ребенка возможности получать уникальный с биологической точки зрения продукт. Даже частичная замена естественного вскармливания обычно приводит к резкому снижению лактации и в итоге – полному переходу на искусственное вскармливание. Во-вторых, многие лечебные смеси просто не соответствуют физиологическим потребностям интенсивно растущего ребенка. Прежде всего это относится к гидролизатам. В-третьих, введение лечебных смесей, как правило, не решает проблему, а без адекватного лечения даже откладывает ее решение и усугубляет ее [14]. Любая система организма, лишенная адекватной рабочей нагрузки, начинает постепенно атрофироваться (например, мышцы при отсутствии физической активности). То же происходит с системами пищеварения и противоаллергической защиты (система адаптации) – лечебные смеси (особенно полные гидролизаты), не создавая адекватной нагрузки на ЖКТ, в итоге приводят к тому, что адаптационные системы организма перестают развиваться и фактически атрофируются. Вследствие этого возникают колоссальные проблемы с введением практически любых новых продуктов, а также сильное обострение пищевой аллергии. Прежде чем рекомендовать лечебное питание, врач должен тщательно оценить целесообразность этого шага и рассмотреть альтернативные возможности. В случае лактазной недостаточности определяющим фактором является клиническая картина и состояние ребенка: если лактазная недостаточность компенсирована (ребенок не отстает в физическом развитии, у него нет выраженной диареи и болевого синдрома), питание лучше не менять (лечебные смеси не вводить).
Вследствие этого возникают колоссальные проблемы с введением практически любых новых продуктов, а также сильное обострение пищевой аллергии. Прежде чем рекомендовать лечебное питание, врач должен тщательно оценить целесообразность этого шага и рассмотреть альтернативные возможности. В случае лактазной недостаточности определяющим фактором является клиническая картина и состояние ребенка: если лактазная недостаточность компенсирована (ребенок не отстает в физическом развитии, у него нет выраженной диареи и болевого синдрома), питание лучше не менять (лечебные смеси не вводить).
При пищевой аллергии, как правило, причиной являются дисбактериоз кишечника и ферментативная незрелость [15]. В большинстве случаев такие состояния лечатся без изменений питания (ребенок остается на естественном вскармливании или продолжает получать обычную олочную смесь). Если ребенок находится на естественном вскармливании (и ГМ достаточно), то практически всегда желательно не рекомендовать лечебное питание, а искать альтернативные способы, например, введение фермента лактазы. Лечебное питание может быть рекомендовано в декомпенсированных случаях как вынужденная крайняя временная мера, но не вместо терапии. При этом нужно стремиться к тому, чтобы со временем питание ребенка стало обычным, соответствующим возрасту [16].
Лечебное питание может быть рекомендовано в декомпенсированных случаях как вынужденная крайняя временная мера, но не вместо терапии. При этом нужно стремиться к тому, чтобы со временем питание ребенка стало обычным, соответствующим возрасту [16].
При невозможности вскармливания ребенка ГМ или адаптированной смесью на основе коровьего молока основной альтернативой является введение смеси на основе козьего молока. Если не получается ввести смесь на козьем молоке (что бывает достаточно редко), можно рекомендовать введение соевой смеси.
Правила введения докорма
Введение новой смеси должно быть очень постепенным: начиная с 10–20 г в кормление, каждый день прибавлять еще по 20–30 г до нужного количества. При этом необходимо обращать внимание на переносимость этой смеси, учитывая не только изменения стула или аллергические реакции, но и нравится ли ребенку данная смесь. При смешанном вскармливании сначала кормить ГМ, а затем – смесью. Для кормящей женщины может быть удобнее чередовать кормления грудью и смесью. Такой вариант смешанного вскармливания допустим, но существует риск, что ребенок может отказаться от груди.
Такой вариант смешанного вскармливания допустим, но существует риск, что ребенок может отказаться от груди.
Нужно оценивать изменения от исходного состояния. Смесь подходит, если ее введение не вызывает ухудшения состояния и самочувствия ребенка. Не стоит рассчитывать, что введение смеси решит какие-то проблемы, например, избавит ребенка от запоров или колик. Даже при введении специальных смесей этого чаще всего не происходит без адекватного лечения. Если при введении смеси возникло ухудшение (кожные высыпания появились или усилились, ухудшился стул, больше стало болей в животе и беспокойства), не нужно сразу отказываться от этой смеси – 2-4 дня продолжать давать ее в том же количестве, не увеличивая. Если ухудшение не проходит, следует попробовать другую (также постепенно). Поэтому не рекомендуется покупать сразу много новой смеси, а для пробы взять одну упаковку. Если смесь не вызвала у ребенка проблем и на вкус малышу нравится, менять ее нежелательно, даже вредно, поэтому нужно сразу выбирать такую смесь, которая будет устраивать по цене и доступности.
Если одна смесь меняется на другую (например, при смене ступени с первой на вторую, а также при замене лечебной смеси на обычную), это также нужно делать постепенно: в первый день меняется одна мерная ложка (30 г готовой смеси) в каждое кормление, на второй день – вторая и т. д. При этом допустимо смешивать старую и новую смесь в одной бутылке.
В экстренных ситуациях, когда нужно срочно вводить смесь вместо ГМ (медицинские показания у кормящей мамы, резкое убывание ГМ), тоже желательно максимально, насколько это возможно, придерживаться принципа постепенности введения. Не исключено, что безопаснее для ребенка будет введение неполного количества смеси при более частом кормлении с постепенным доведением количества до необходимого. В такой ситуации для облегчения адаптации возможно применение пробиотиков и/или ферментных препаратов, а также антигистаминных препаратов коротким курсом.
Для детей до 4-5 месяцев введение любого нового продукта является стрессом, поэтому одно из главных правил вскармливания в этом возрасте состоит в следующем: без необходимости смесь не менять [17].
Если ребенок вскармливается полным или частичным гидролизатом либо аминокислотной смесью, нужно стремиться к переходу на обычную смесь либо на смесь на основе козьего молока. Очень часто без такого перехода не удается избавиться от проблем с пищеварением у детей, получающих лечебное питание (за исключением смесей на козьем молоке), поскольку гидролизаты тормозят развитие системы пищеварения и микробиоценоза кишечника.
КОНФЛИКТ ИНТЕРЕСОВ. Авторы статьи подтвердили отсутствие конфликта интересов, о котором необходимо сообщить.
CONFLICT OF INTERESTS. Not declared.
Литература/References
- Лукоянова О. Л. Грудное молоко как эталонная модель для создания детских молочных смесей // Вопросы современной педиатрии. 2012; 4: 111-115. [Lukoyanova O. L. Grudnoye moloko kak etalonnaya model’ dlya sozdaniya detskikh molochnykh smesey [Breast milk as a reference model for the creation of infant formula] // Voprosy sovremennoy pediatrii.
 2012; 4: 111-115.]
2012; 4: 111-115.] - Лукоянова О. Л., Боровик Т. Э., Скворцова В. А., Беляева И. А., Бушуева Т. В., Звонкова Н. Г., Яцык Г. В. Состав грудного молока и питание матери: есть связь? // Педиатрия. Журнал им. Г. Н. Сперанского. 2018; 4 (97): 160-167. [Lukoyanova O. L., Borovik T. E., Skvortsova V. A., Belyayeva I. A., Bushuyeva T. V., Zvonkova N. G., Yatsyk G. V. Sostav grudnogo moloka i pitaniye materi: yest’ svyaz’? [Breast milk composition and maternal nutrition: is there a connection?] // Pediatriya. Zhurnal im. G. N. Speranskogo. 2018; 4 (97): 160-167.]
- Martinez-Ferez A., et al. Goats’ milk as a natural source of lactose derived oligosaccharides // International Dairy Journal. 2006; 16 (2): 173-181.
- Sousa Y. R. F., et al. Composition and isolation of goat cheese whey oligosaccharides by membrane technology // Int J Biol Macromal. 2019; 139 (1): 57-62.
- Pellis L. T, and B. H. Naturally high content of nucleotides in goat milk based infant formula.
 Poster presented at ESPGHAN, Geneva, Switzerland, 2018.
Poster presented at ESPGHAN, Geneva, Switzerland, 2018. - Боровик Т. Э., Лукоянова О. Л., Семенова Н. Н., Звонкова Н. Г., Бушуева Т. В., Степанова Т. Н., Скворцова В. А., Мельничук О. С., Копыльцова Е. А., Семикина Е. Л., Захарова И. Н., Рюмина И. И., Нароган М. В., Грошева Е. В., Ханферьян Р. А., Савченко Е. А., Белоусова Т. В., Елкина Т. Н., Суровикина Е. А., Татаренко Ю. А. Эффективность использования адаптированной смеси на совное козьего молока в питании здоровых детей первого полугодия жизни: результаты многоцентрового проспективного сравнительного исследования // Вопросы современной педиатрии. 2017; 3 (16). [Borovik T. E., Lukoyanova O. L., Semenova N. N., Zvonkova N. G., Bushuyeva T. V., Stepanova T. N., Skvortsova V. A., Mel’nichuk O. S., Kopyl’tsova Ye. A., Semikina Ye. L., Zakharova I. N., Ryumina I. I., Narogan M. V., Grosheva Ye. V., Khanfer’yan R. A., Savchenko Ye. A., Belousova T. V., Yelkina T. N., Surovikina Ye. A., Tatarenko Yu. A. Effektivnost’ ispol’zovaniya adaptirovannoy smesi na sovnoye koz’yego moloka v pitanii zdorovykh detey pervogo polugodiya zhizni: rezul’taty mnogotsentrovogo prospektivnogo sravnitel’nogo issledovaniya [The effectiveness of the use of an adapted mixture of goat milk in the diet of healthy children in the first half of life: the results of a multicenter prospective comparative study] // Voprosy sovremennoy pediatrii.
 2017; 3 (16).]
2017; 3 (16).] - Сафронова А. И., Коновалова Л. С., Гурченкова М. А. Современные подходы к адаптации молочных смесей для детей раннего возраста // Вопросы современной педиатрии. 2012; 2 (11): 56-61. [Safronova A. I., Konovalova L. S., Gurchenkova M. A. Sovremennyye podkhody k adaptatsii molochnykh smesey dlya detey rannego vozrasta. [Modern approaches to the adaptation of infant formula for young children] // Voprosy sovremennoy pediatrii. 2012; 2 (11): 56-61.]
- Захарова И. Н., Дмитриева Ю. А., Гордеева Е. А. Совершенствование детских молочных смесей – на пути приближения к женскому молоку // Медицинский совет. 2016; 1: 90-97. [Zakharova I. N., Dmitriyeva Yu. A., Gordeyeva Ye. A. Sovershenstvovaniye detskikh molochnykh smesey – na puti priblizheniya k zhenskomu moloku. [Improving baby milk formulas – on the way to approaching human milk] // Meditsinskiy sovet. 2016; 1: 90-97.]
- Luukkainen P., Salo M. K., Nikkari T. The fatty acid composition of banked human milk and infant formulas: The choices of milk for feeding preterm infants // European Journal of Pediatrics. 1995. V. 154. № 4. P. 316-319.
- Vandenplas Y., Alarcon P., Fleischer D., Hernell O., Kolacek S., Laignelet H., Lönnerdal B., Raman R., Rigo J., Salvatore S., Shamir R., Staiano A., Szajewska H., Van Goudoever H. J., von Berg A., Lee Way S. Should Partial Hydrolysates Be Used as Starter Infant Formula? A Working Group Consensus // Journal of Pediatric Gastroenterology and Nutrition. 2016. Vol. 62. Issue 1. Р. 22-35.
- Специализированные продукты питания для детей с различной патологией. Каталог. Изд. 2-е / Под ред. Боровик Т. Э., Ладодо К. С., Скворцовой В. А. М.: МИА, 2008. 272 с. [Spetsializirovannye produkty pitaniya dlya detey s razlichnoy patalogiey [Special nutrition for children with different pathologies] Catalogue. 2nd edition / Edited by Borovik T. E., Ladodo K. S., Skvortsova V. A. Moscow: MIA, 2008. 272 p.]
- Ревякина В. А., Боровик Т. Е. Пищевая аллергия у детей: современные аспекты // Российский аллергологический журнал. 2004; 2: 71-77. [Revyakina V. A., Borovik T. E. Pischevaya allergiya u detey: sovremennye aspekty [Food allergy in children: modern aspects] // Rossiysky allergologichesky zhurnal. 2004; 2: 71-77.]
- Богданова Н. М., Булатова Е. М. Физиологическое обоснование выбора стартовых формул для вскармливания рожденного в срок ребенка при наличии противопоказаний к грудному вскармливанию // Вопросы современной педиатрии. 2007; 4 (6): 91-100. [Bogdanova Н. M., Bulatova Ye. M. Fiziologicheskoye obosnovaniye vybora startovykh formul dlya vskarmlivaniya rozhdennogo v srok rebenka pri nalichii protivopokazaniy k grudnomu vskarmlivaniyu. [Physiological rationale for the choice of starting formulas for feeding a child born on time in the presence of contraindications to breastfeeding] // Voprosy sovremennoy pediatrii. 2007; 4 (6): 91-100.]
- Боровик Т. Э. и др. Подходы к организации диетотерапии детям первого года жизни с пищевой аллергией в современных условиях // Доктор.Ру. 2009; 2: 34-40. [Borovik T. E. et al. Podkhody k organizatsii dietoterapii detyam pervogo goda zhizni s pischevoy allergiey v sovremennykh usloviyakh [Approaches to dietary therapy for children of the first year of life with food allergy under modern conditions] // Doctor.ru. 2009; 2: 34-40.]
- Копанев Ю. А., Соколов А. Л. Дисбактериоз у детей. М.: ОАО «Издательство «Медицина», 2008. 128 с. [Kopanev Yu. A., Sokolov A. L. Дисбактериоз Disbakterioz u detey [Dysbacteriosis in children] Moscow: Izdatelstvo Meditsina JSC, 2008. 128 p.]
- Копанев Ю. А., Соколов А. Л. Атопический дерматит у детей раннего возраста. Нарушение адаптации. Целесообразность введения лечебных смесей // Лечащий Врач. 2020; 6: 7-11. [Kopanev Yu. A., Sokolov A. L. Atopicheskiy dermatit u detey rannego vozrasta. narusheniye adaptatsii. tselesoobraznost’ vvedeniya lechebnykh smesey. [Atopic dermatitis in young children. Violation of adaptation. The expediency of introducing therapeutic mixtures] // The Lechaschi Vrach Journal. 2020; 6: 7-11.]
- Боровик Т. Э. и др. Национальная стратегия вскармливания детей первого года жизни в Российской Федерации // Практика педиатра. 2008; 1: 13-17. [Borovik T. E. et al. Natsionalnaya strategiya vskarmlivaniya detey pervogo goda zhizni v rossiyskoy federatsii [National strategy of feeding children of the first year of life in the Russian Federation] // Praktika pediatra. 2008; 1: 13-17.]
Ю. А. Копанев1, кандидат медицинских наук
А. Л. Соколов
ФБУН МНИИЭМ им. Г. Н. Габричевского Роспотребнадзора, Москва, Россия
1Контактная информация: [email protected]
DOI: 10.26295/OS.2021.75.40.010
Алгоритмы, принципы и оптимальные сроки введения адаптированных и специализированных смесей для вскармливания детей грудного возраста/ Ю. А. Копанев, А. Л. Соколов
Для цитирования: Копанев Ю. А., Соколов А. Л. Алгоритмы, принципы и оптимальные сроки введения адаптированных и специали-
зированных смесей для вскармливания детей грудного возраста // Лечащий Врач. 2021; 2 (24): 49-52.
Теги: новорожденные, дети младшего возраста, молочные смеси, питание
НОУ ИНТУИТ | Введение в схемы, автоматы и алгоритмы
Форма обучения:
дистанционная
Стоимость самостоятельного обучения:
бесплатно
Доступ:
свободный
Документ об окончании:
Уровень:
Специалист
Длительность:
14:18:00
Выпускников:
102
Качество курса:
5.00 | 5.00
Краткий начальный курс по таким дискретным структурам как схемы, конечные автоматы и алгоритмы.
Курс знакомит с двумя представлениями булевых функций с помощью специальных классов ориентированных графов без циклов: логическими схемами (схемами из функциональных элементов) и упорядоченными бинарными диаграммами решений (УБДР).
Изложены основы теории конечных автоматов: конечные автоматы-преобразователи и -распознаватели, детерминированные автоматы и языки, недетерминированные автоматы и их детерминизация, регулярные выражения и языки, синтез конечного автомата по регулярному выражению, замкнутость класса автоматных языков относительно разных операций, теорема о разрастании для автоматных языков, примеры неавтоматных языков.
Дается краткое введение в теорию алгоритмов, сравниваются три формальных модели описания алгоритмов: структурированные программы, частично рекурсивные функции и машины Тьюринга, формулируется тезис Тьюринга-Черча и устанавливается алгоритмическая неразрешимость ряда проблем, относящихся к свойствам структурированных программ.
Решение большинства рассматриваемых в курсе проблем доведено до уровня алгоритмических процедур и проиллюстрировано на примерах. Каждая лекция завершается разделом с задачами и упражнениями, позволяющими закрепить пройденный материал.
ISBN: 978-5-94774-714-0
Теги: PQ, автоматы, алгоритмы, арифметическая функция, вычисления, вычислимость, диаграмма автомата, законы, компоненты, курсы, полустепень исхода, примитивная рекурсия, примитивно рекурсивная функция, рабочая переменная, распознаватель, регулярные выражения, сложность, структурированная программа, УБДР, элементы
Предварительные курсы
Дополнительные курсы
2 часа 30 минут
—
Предварительные сведения
Класс \mathcal{P}_n булевых функций от n переменных. Задание булевых функций с помощью таблиц. Булевы функции от 1-ой и 2-х
переменных. Булевы (логические) формулы и их
эквивалентность. Основные эквивалентности ( законы логики ).
Дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ).
Графы. Деревья.
—
Реализация булевых функций с помощью логических схем
Логические схемы (схемы из функциональных элементов) и реализуемые ими функции. Задачи синтеза и анализа схем. Логические схемы и линейные программы. Примеры логических схем: сложение по модулю 2 и двоичный сумматор
—
Упорядоченные бинарные диаграммы решений (УБДР)
Бинарные деревья решений и их превращение в упорядоченные бинарные
диаграммы решений (УБДР). Сокращенные УБДР и их построение по произвольным
УБДР, алгоритм СОКРАЩЕНИЕ-УБДР. Построение сокращенных УБДР по формулам
—
Конечные автоматы: преобразователи и распознаватели
Конечные автоматы-преобразователи. Пример: сложение двоичных чисел.
Конечные автоматы-распознаватели. Конечно-автоматные языки. Доказательство
правильности автомата. Произведение автоматов. Замкнутость класса конечно-автоматных языков
относительно теоретико-множественных операций
—
Регулярные языки и конечные автоматы
Операции конкатенации и итерации языков. Регулярные выражения и языки. Примеры регулярных выражений и языков. Построение конечного автомата по регулярному выражению
—
Алгоритмы: частично рекурсивные функции
Операторы суперпозиции, примитивной рекурсии и минимизации. Классы частично
рекурсивных и примитивно рекурсивных функций. Программная вычислимость
частично рекурсивных функций. Рекурсивность табличных функций, функций, определенных с помощью суммирования и произведения, кусочно заданных функций, функций нумерации n-ок и
функций, определенных совместной рекурсией
—
Алгоритмы: машины Тьюринга
Определение машин Тьюринга и класса вычислимых ими функций. Примеры работы машин Тьюринга.
Тьюрингово программирование: последовательная и параллельная композиция, ветвление
(условный оператор), повторение (оператор цикла)
—
Вычислимые функции, тезис Тьюринга-Черча и неразрешимые проблемы
Частично рекурсивные функции вычислимы на м.Т. М.Т. моделируют структурированные программы.
Классы частично рекурсивных функций,
функций, вычислимых структурированными программами, и функций, вычислимых
машинами Тьюринга, совпадают. Тезис Тьюринга-Черча. Алгоритмически разрешимые и неразрешимые
проблемы. Неразрешимость проблем самоприменимости, останова, тотальности, эквивалентности
и оптимизации текста программ
—
Введение в понятие алгоритма
☰
Понятие алгоритма
В сегодняшнем социуме слово «алгоритм» настолько широко распространено, что большинству интуитивно понятно. Под ним мы понимаем какую-либо последовательность шагов для достижения той или иной цели. Однако для теоретической науки понятие «алгоритма» достаточно сложное.
Считается, что однозначного определения алгоритма нет, хотя в основном различные источники дают очень близкие определения.
Итак, в широко распространенных определениях алгоритма (в рамках школьного курса информатики) можно выделить следующие составляющие:
Алгоритм – это конечная последовательность указаний …
- … на языке понятном исполнителю, …
- … задающая процесс решения задач определенного типа …
- … и ведущая к получению результата, однозначно определяемого допустимыми исходными данными.
В последнем пункте определения говорится о том, что результат выполнения алгоритма напрямую зависит от исходных данных. Т.е. один и тот же алгоритм при разных исходных данных даст разные результаты. С другой стороны, если одному и тому же алгоритму передать несколько раз одни и те же данные, он должен столько же раз выдать один и тот же результат.
Слово «алгоритм» происходит от имени ученого IX века Муххамеда бен Аль-Хорезми («аль-хорезми» -> «алгоритм»), который описал правила выполнения арифметических действий в десятичной системе счисления. Словом «алгоритм» потом и стали обозначать эти правила вычислений. Однако с течением времени понятие алгоритма видоизменялось и в XX веке под ним стали понимать какую-либо последовательность действий, приводящую к решению поставленной задачи.
Сначала определение понятия алгоритма было проблемой математики, однако с течением времени теория алгоритмов стала развиваться за счет влияния открытий не только в математике, но и в информатике. В настоящее время алгоритм является одним из главных понятий информатики.
Другими словами, следует понимать, что первоначально теория алгоритмов возникла в математике и представляла собой поиск способов решения задач определенного типа посредством определенного набора указаний.
Свойства алгоритма
- Дискретность (в данном случае, разделенность на части) и упорядоченность. Алгоритм должен состоять из отдельных действий, которые выполняются последовательно друг за другом.
- Детерминированность (однозначная определенность). Многократное применение одного алгоритма к одному и тому же набору исходных данных всегда дает один и тот же результат.
- Формальность. Алгоритм не должен допускать неоднозначности толкования действий для исполнителя.
- Результативность и конечность. Работа алгоритма должна завершаться за определенное число шагов, при этом задача должна быть решена.
- Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.
Исполнитель и разработчик алгоритма
Разрабатывать, придумывать алгоритмы могут только разумные существа (например, человек). А вот формально (не думая и не оценивая) исполнять, могут какие-либо машины (например, компьютеры, бытовые приборы). В чем польза такого разделения труда? Дело в том, что человек освобождается от рутинной деятельности, которая часто может занимать много времени, и поручает ее машинам.
Однако машины не люди: приборы понимают лишь ограниченное число команд и могут обрабатывать данные (объекты) далеко не всех типов. Отсюда следует, что разработчик алгоритма в конечном итоге должен описать алгоритм в допустимых командах определенного исполнителя (той машины, которой будет поручено выполнение алгоритма). Совокупность команд, которые данный исполнитель может выполнять, называется системой команд исполнителя. Объекты (данные), над которыми исполнитель может выполнять действия, формируют среду исполнителя.
Язык программирования — средство записи алгоритмов для компьютеров
Достаточно универсальным исполнителем является компьютер. С его помощью можно выполнять разнообразные по видам алгоритмы: делать математические вычисления, обрабатывать текстовые данные, изменять графику и др. В каком-то смысле компьютер может делать многое, что и человек, а некоторые вещи намного быстрее. Однако человек и компьютер «разговаривают» на совершенно разных языках: один – на естественном (русском, английском и др.), а другой – на формальном (машинном) языке.
Разработав алгоритм, человек должен как-то «объяснить» его компьютеру. Для этих целей служат языки программирования, а результатом записи алгоритма на них является программа.
В настоящее время язык программирования – это скорее некий посредник между человеком и вычислительной машиной. Программа, написанная на языке программирования, в последствии переводится на машинный язык транслятором.
Итог
Изучение алгоритмов имеет большую практическую значимость. Это связано с тем, что создание алгоритма предполагает подробное описание каждого шага решения задачи, и в конечном итоге шаг алгоритма может быть достаточно прост для выполнения его компьютером. А значит, задачи, для которых можно выработать алгоритм их решения, могут быть автоматизированы, т.е. переложены «на плечи» машин.
Однако следует всегда помнить, что не все задачи имеют алгоритмическое решение.
При этом для тех задач, которые все-таки имеют алгоритмическое решение, могут быть разработаны различные алгоритмы. Но наиболее эффективным, скорее всего, будет только один.
Теория алгоритмов. Введение в сложность вычислений
В настоящем учебном пособии даны основные идеи и методы теории сложности вычислений. В нем представлены вычислительные возможности, схемы моделирования языков программирования машинами Тьюринга, а также сложностные классы задач.
Укажите параметры рабочей программы
Дисциплина
Математическая логика и теория алгоритмов
УГС
09.00.00 «ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА»10.00.00 «ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ»02.00.00 «КОМПЬЮТЕРНЫЕ И ИНФОРМАЦИОННЫЕ НАУКИ»01.00.00 «МАТЕМАТИКА И МЕХАНИКА»15.00.00 «МАШИНОСТРОЕНИЕ»44.00.00 «ОБРАЗОВАНИЕ И ПЕДАГОГИЧЕСКИЕ НАУКИ»23.00.00 «ТЕХНИКА И ТЕХНОЛОГИИ НАЗЕМНОГО ТРАНСПОРТА»27.00.00 «УПРАВЛЕНИЕ В ТЕХНИЧЕСКИХ СИСТЕМАХ»12.00.00 «ФОТОНИКА, ПРИБОРОСТРОЕНИЕ, ОПТИЧЕСКИЕ И БИОТЕХНИЧЕСКИЕ СИСТЕМЫ И ТЕХНОЛОГИИ»38.00.00 «ЭКОНОМИКА И УПРАВЛЕНИЕ»11.00.00 «ЭЛЕКТРОНИКА, РАДИОТЕХНИКА И СИСТЕМЫ СВЯЗИ»45.00.00 «ЯЗЫКОЗНАНИЕ И ЛИТЕРАТУРОВЕДЕНИЕ»
Направление подготовки
Уровень подготовки
Кормен, Томас Х .: 8601419521876: Amazon.com: Книги
«
» В свете стремительного роста объема данных и разнообразия вычислительных приложений эффективные алгоритмы необходимы сейчас как никогда. Эта красиво написанная, тщательно организованная книга является исчерпывающим вводным пособием по проектированию и анализу алгоритмов. Первая половина предлагает эффективный метод обучения и изучения алгоритмов; вторая половина затем привлекает более продвинутых читателей и любопытных студентов с убедительным материалом как о возможностях, так и о проблемах в этой увлекательной области.»- Шан-Хуа Тенг, Университет Южной Калифорнии
» «Введение в алгоритмы», «библия» в данной области, представляет собой исчерпывающий учебник, охватывающий весь спектр современных алгоритмов: от самых быстрых алгоритмов и структур данных до полиномиальных. временные алгоритмы для кажущихся неразрешимыми проблем, от классических алгоритмов теории графов до специальных алгоритмов сопоставления строк, вычислительной геометрии и теории чисел. В пересмотренное третье издание примечательно добавлена глава о деревьях Ван Эмде Боаса, одной из наиболее полезных структур данных, и о многопоточных алгоритмах — теме, которая становится все более важной.»- Дэниел Спилман, факультет компьютерных наук Йельского университета
» Как преподаватель и исследователь в области алгоритмов на протяжении более двух десятилетий, я могу однозначно сказать, что книга Кормена — лучший учебник, который я когда-либо видел по этому поводу. предмет. Он предлагает проницательный, энциклопедический и современный подход к алгоритмам, и наш отдел будет продолжать использовать его для обучения как на уровне магистратуры, так и на уровне бакалавриата, а также в качестве надежного справочного материала для исследований ». — Габриэль Робинс, Департамент компьютерных наук, Университет Вирджинии
Введение в алгоритмы , «библия» в этой области, представляет собой исчерпывающий учебник, охватывающий весь спектр современных алгоритмов: от самых быстрых алгоритмов и структур данных до алгоритмов с полиномиальным временем для кажущихся неразрешимыми проблем, от классических алгоритмов теории графов специальным алгоритмам сопоставления струн, вычислительной геометрии и теории чисел.В пересмотренное третье издание примечательно добавлена глава о деревьях Ван Эмде Боаса, одной из наиболее полезных структур данных, и о многопоточных алгоритмах — теме, которая становится все более важной.
— Дэниел Спилман, , факультет компьютерных наук, Йельский университет
Об авторе
Томас Х. Кормен — профессор компьютерных наук и бывший директор Института письма и риторики Дартмутского колледжа. Он является соавтором (вместе с Чарльзом Э. Лейзерсоном, Рональдом Л. Ривестом и Клиффордом Штайном) ведущего учебника по компьютерным алгоритмам Introduction to Algorithms (третье издание, MIT Press, 2009).
Чарльз Э. Лейзерсон — профессор компьютерных наук и инженерии Массачусетского технологического института.
Рональд Л. Ривест — профессор электротехники и компьютерных наук Эндрю и Эрны Витерби в Массачусетском технологическом институте.
Клиффорд Штайн — профессор промышленной инженерии и операционных исследований Колумбийского университета.
Введение в алгоритмы: содержание
Томаса Х. Кормена, Чарльза Э.Лейзерсон и Рональд Л. Ривест
ПРЕДИСЛОВИЕ
ГЛАВА 1: ВВЕДЕНИЕ
ЧАСТЬ I: Математические основы
ГЛАВА 2: РАЗВИТИЕ ФУНКЦИЙ
ГЛАВА 3: ИТОГИ
ГЛАВА 4: ПОВТОРЯЕМОСТЬ
ГЛАВА 5: НАБОРЫ И Т.Д.
ГЛАВА 6: ПОДСЧЕТ И ВЕРОЯТНОСТЬ
ЧАСТЬ II: Статистика сортировки и заказа
ГЛАВА 7: ОБЕСПЕЧЕНИЕ
ГЛАВА 8: QUICKSORT
ГЛАВА 9: СОРТИРОВКА В ЛИНЕЙНОМ ВРЕМЕНИ
ГЛАВА 10: МЕДИАНЫ И СТАТИСТИКА ЗАКАЗА
ЧАСТЬ III: Структуры данных
ГЛАВА 11: ЭЛЕМЕНТАРНЫЕ СТРУКТУРЫ ДАННЫХ
ГЛАВА 12: ХЭШ-ТАБЛИЦЫ
ГЛАВА 13: ДВОИЧНЫЕ ПОИСКОВЫЕ ДЕРЕВА
ГЛАВА 14: КРАСНО-ЧЕРНЫЕ ДЕРЕВА
ГЛАВА 15: ДОПОЛНИТЕЛЬНЫЕ СТРУКТУРЫ ДАННЫХ
ЧАСТЬ IV: Расширенные методы проектирования и анализа
ГЛАВА 16: ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
ГЛАВА 17: ЖАДНЫЕ АЛГОРИТМЫ
ГЛАВА 18: АМОРТИЗИРОВАННЫЙ АНАЛИЗ
ЧАСТЬ V: Расширенные структуры данных
ГЛАВА 19: ДЕРЕВЬЯ B
ГЛАВА 20: БИНОМИАЛЬНЫЕ БОЛЕЗНИ
ГЛАВА 21: ВОЛНЫ ФИБОНАЧЧИ
ГЛАВА 22: СТРУКТУРЫ ДАННЫХ ДЛЯ РАЗЪЕДИНЕННЫХ НАБОРОВ
ЧАСТЬ VI: Графические алгоритмы
ГЛАВА 23: ЭЛЕМЕНТАРНЫЕ АЛГОРИТМЫ ГРАФИКОВ
ГЛАВА 24: МИНИМАЛЬНЫЕ ДЕРЕВЯННЫЕ ДЕРЕВЬЯ
ГЛАВА 25: НАИБОЛЕЕ КОРОТКИЕ ПУТИ К ОДНОИСТОЧНИКУ
ГЛАВА 26: НАИБОЛЕЕ КОРОТКИЕ ПУТИ ДЛЯ ВСЕХ ПАР
ГЛАВА 27: МАКСИМАЛЬНЫЙ ПОТОК
ЧАСТЬ VII: Избранные темы
ГЛАВА 28: СОРТИРОВОЧНЫЕ СЕТИ
ГЛАВА 29: АРИФМЕТИЧЕСКИЕ ЦЕПИ
ГЛАВА 30: АЛГОРИТМЫ ДЛЯ ПАРАЛЛЕЛЬНЫХ КОМПЬЮТЕРОВ
ГЛАВА 31: ОПЕРАЦИИ С МАТРИЦЕЙ
ГЛАВА 32: ПОЛИНОМЫ И БПФ
ГЛАВА 33: Теоретико-числовые алгоритмы
ГЛАВА 34: СООТВЕТСТВИЕ СТРОК
ГЛАВА 35: ВЫЧИСЛИТЕЛЬНАЯ ГЕОМЕТРИЯ
ГЛАВА 36: НЕПОЛНОСТЬЮ
ГЛАВА 37: АЛГОРИТМЫ ПРИБЛИЖЕНИЯ
БИБЛИОГРАФИЯ
Краткое изложение курса MIT Introduction to Algorithms
Как вы все, возможно, знаете, я просмотрел и разместил свои конспекты лекций по всему курсу «Введение в алгоритмы» Массачусетского технологического института.В этом посте я хочу обобщить все темы, затронутые на лекциях, и выделить в них некоторые из самых интересных вещей.
На самом деле, до того, как я написал эту статью, я начал писать статью под названием « Самые крутые вещи, которые я узнал из Введение в алгоритмы Массачусетского технологического института», но быстро понял, что то, что я делаю, это перечисление тем в каждой статье, а не действительно указываю на самые крутые вещи . Поэтому я решил сначала написать сводную статью (я обещал это сделать), а уже потом писать статью на действительно самые интересные темы.
Говоря о резюме, я просмотрел в общей сложности 23 лекции, результатом которых стало 14 сообщений в блоге. На то, чтобы опубликовать их здесь, у меня ушел почти год. Вот список всех сообщений:
Я сейчас пройдусь по каждой лекции. Для понимания им требуется немного математических знаний. Если вы не уверены в своих математических навыках, я бы посоветовал прочитать книгу Кнута «Конкретная математика». Он содержит абсолютно всю математику, необходимую для понимания этого курса.
Лекция 1: Анализ алгоритмов
Если вы студент или даже не студент, вы никогда не должны пропустить первую лекцию любого курса! Первая лекция расскажет вам, чего ожидать от курса, как он будет преподаваться, что он будет охватывать, кто профессор, каковы предварительные условия, а также множество других важных и интересных вещей.
В этой лекции вы также познакомитесь с профессором Чарльзом Э. Лейзерсоном (автором CLRS), и он разъяснит следующие темы:
- Зачем изучать алгоритмы и их производительность?
- Что такое анализ алгоритмов?
- Что может быть важнее производительности алгоритмов?
- Проблема сортировки.
- Алгоритм сортировки вставкой.
- Анализ времени работы вставляемой сортировки.
- Асимптотический анализ.
- Анализ времени работы наихудшего, среднего и лучшего случая.
- Анализ наихудшего времени выполнения сортировки при вставке.
- Асимптотическая запись — тета-запись -?.
- Алгоритм сортировки слиянием.
- Рекурсивный характер алгоритма сортировки слиянием.
- Повторение времени выполнения для сортировки слиянием.
- Рекурсионные деревья.
- Анализ времени выполнения сортировки слиянием по дереву рекурсии.
- Общая повторяемость алгоритмов «разделяй и властвуй».
Мне лично интересен список вещей, которые могут быть важнее производительности программы. Это модульность, корректность, ремонтопригодность, безопасность, функциональность, надежность, удобство использования, время программиста, простота, расширяемость, надежность, масштабируемость.
Перейдите по этой ссылке, чтобы увидеть полный обзор первой лекции.
Лекция 2: Анализ алгоритмов (продолжение)
Вторую лекцию читает Эрик Демейн.Он самый молодой профессор в истории Массачусетского технологического института.
Вот темы, которые он объясняет во второй лекции:
- Асимптотические обозначения.
- Обозначение Big-o — О.
- Установить определение O-нотации.
- Обозначение заглавной буквы и омеги -?.
- Тета-нотация -?.
- Строчные обозначения — o.
- Строгое обозначение омеги -?.
- Решение повторений методом подстановки.
- Решение повторений методом дерева рекурсии.
- Решение рецидивов по методике Мастера.
- Интуитивно понятный эскиз метода Мастера.
В этой лекции интересно провести аналогию (O,?,?, O,?) С (?,?, =, <,>).
Например, если мы скажем f (n) = O (n 2 ), то, используя аналогию, мы можем думать об этом как о f (n)? c · n 2 , то есть функция f (n) всегда меньше или равна c · n 2 , или, другими словами, она ограничена сверху функцией c · n 2 , что и есть f (n) = O (n 2 ) означает.
Перейдите по этой ссылке, чтобы получить полный обзор второй лекции.
Лекция 3: Разделяй и властвуй
Третья лекция посвящена методу разработки алгоритма «разделяй и властвуй» и его приложениям. Метод «разделяй и властвуй» решает задачу: 1) разбивая ее на несколько подзадач (шаг разделения), 2) рекурсивно решая каждую проблему (шаг «побеждай»), 3) комбинируя решения (шаг объединения).
Вот темы, объясненные в третьей лекции:
- Природа алгоритмов «разделяй и властвуй».
- Пример «разделяй и властвуй» — сортировка слиянием.
- Расчет времени выполнения сортировки слиянием по методу Мастера.
- Бинарный поиск.
- Питание числа.
- числа Фибоначчи.
- Алгоритмы вычисления чисел Фибоначчи.
- Фибоначчи по наивному рекурсивному алгоритму.
- Фибоначчи по восходящему алгоритму.
- Фибоначчи методом наивного рекурсивного возведения в квадрат.
- Метод Фибоначчи матричным рекурсивным возведением в квадрат.
- Умножение матриц
- Алгоритм Штрассена.
- Проблема компоновки СБИС (очень крупномасштабная интеграция).
Больше всего меня впечатлили четыре алгоритма вычисления чисел Фибоначчи. На самом деле я написал об одном из них в своей публикации «Об алгоритме линейного времени для поиска чисел Фибоначчи», в которой объясняется, как этот алгоритм на самом деле является квадратичным на практике (но линейным в теории).
Перейдите по этой ссылке, чтобы увидеть полный обзор третьей лекции.
Лекция 4: Сортировка
Четвертая лекция полностью посвящена алгоритму быстрой сортировки. Это стандартный алгоритм, который используется для сортировки в большинстве компьютерных систем. Вы просто должны это знать.
Темы, объясненные в четвертой лекции:
- Разделяй и властвуй подход к сортировке.
- Алгоритм быстрой сортировки.
- Подпрограмма разбиения в алгоритме быстрой сортировки.
- Анализ времени работы быстрой сортировки.
- Анализ наихудшего случая быстрой сортировки.
- Интуитивно понятный и точный анализ быстрой сортировки.
- Рандомизированная быстрая сортировка.
- Индикатор случайных величин.
- Анализ времени выполнения рандомизированной быстрой сортировки в ожидании.
Мне понравилось, как идея рандомизации подпрограммы разбиения в алгоритме быстрой сортировки привела к тому, что время выполнения не зависит от порядка элементов. Детерминированная быстрая сортировка всегда может получать входные данные, которые запускают наихудшее время работы O (n 2 ), но наихудшее время работы рандомизированной быстрой сортировки определяется только выходными данными генератора случайных чисел.
Однажды я написал еще один пост о быстрой сортировке под названием «Три прекрасных быстрой сортировки», в котором я резюмировал то, что сказал Джон Бентли об экспериментальном анализе времени выполнения быстрой сортировки и о том, как текущий алгоритм быстрой сортировки выглядит в отраслевых библиотеках (таких как стандартная библиотека c, которая предоставляет функцию qsort).
Перейдите по этой ссылке, чтобы увидеть полный обзор четвертой лекции.
Лекция 5: Сортировка (продолжение)
Пятая лекция продолжается о сортировке и исследует, что ограничивает время выполнения сортировки до O (n · lg (n)).Затем он выходит за рамки этого ограничения и показывает несколько алгоритмов линейной сортировки по времени.
Темы, объясненные в пятой лекции:
- Как быстро мы можем сортировать?
- Сравнительная модель сортировки.
- Деревья решений.
- Алгоритмы сортировки сравнением, основанные на деревьях решений.
- Нижняя оценка для сортировки дерева решений.
- Сортировка за линейное время.
- Счетная сортировка.
- Концепция стабильной сортировки.
- Сортировка по основанию.
- Корректность сортировки по основанию системы счисления.
- Анализ времени выполнения радииксной сортировки.
Самой интересной темой здесь было то, как любой алгоритм сортировки сравнения может быть преобразован в дерево решений (и наоборот), что ограничивает скорость сортировки.
Перейдите по этой ссылке, чтобы увидеть полный обзор пятой лекции.
Лекция 6: Статистика заказов
Шестая лекция посвящена проблеме статистики порядка — как найти k-й наименьший элемент среди n элементов.Наивный алгоритм состоит в том, чтобы отсортировать список из n элементов и вернуть k-й элемент в отсортированном списке, но при таком подходе он выполняется за время O (n · lg (n)). Эта лекция показывает, как можно построить рандомизированный алгоритм с линейным временем (в ожидании) для этой задачи.
Темы, объясненные в шестой лекции:
- Статистика заказов.
- Алгоритм статистики наивного порядка через сортировку.
- Рандомизированный алгоритм статистики порядка «разделяй и властвуй».
- Анализ ожидаемого времени работы алгоритма статистики рандомизированного порядка.
- Наихудший случай линейной статистики порядка.
Интересным моментом в этой лекции является то, что детерминированный алгоритм линейного времени наихудшего случая для статистики порядка не используется на практике, потому что он плохо работает по сравнению с алгоритмом рандомизированного линейного времени.
Перейдите по этой ссылке, чтобы увидеть полный обзор шестой лекции.
Лекция 7: Хеширование
Это первая из двух лекций по хешированию. Он вводит хеширование и различные стратегии разрешения конфликтов.
Все темы, объясненные в седьмой лекции:
- Проблема с таблицей символов.
- Стол прямого доступа.
- Понятие хеширования.
- Коллизии при хешировании.
- Разрешение конфликтов путем объединения в цепочку.
- Анализ наихудшего и среднего времени поиска цепочки.
- Хеш-функции.
- Хэш-метод деления.
- Метод хеширования умножения.
- Разрешение коллизий путем открытой адресации.
- Стратегии исследования.
- Линейное зондирование.
- Двойное хеширование.
- Анализ открытой адресации.
Перейдите по этой ссылке, чтобы увидеть полный обзор седьмой лекции.
Лекция 8: Хеширование (продолжение)
Вторая лекция по хешированию. Он устраняет слабые места хеширования — для любого выбора хеш-функции существует плохой набор ключей, у которых все хешируются с одним и тем же значением. Злоумышленник может воспользоваться этим и атаковать нашу программу.Универсальное хеширование решает эту проблему. Другая тема, обсуждаемая в этой лекции, — это идеальное хеширование — с учетом n ключей, как построить хеш-таблицу размера O (n), где поиск требует O (1) гарантированно.
Все темы восьмой лекции:
- Слабость хеширования.
- Универсальное хеширование.
- Построение универсальных хеш-функций.
- Идеальное хеширование.
- Неравенство Маркова.
Перейдите по этой ссылке, чтобы увидеть полный обзор восьмой лекции.
Лекция 9: Поисковые деревья
В этой лекции в первую очередь обсуждаются произвольно построенные деревья двоичного поиска. (Предполагается, что вы знаете, что такое бинарные деревья.) Подобно универсальному хешированию (см. Предыдущую лекцию), они решают проблему, когда вам нужно построить дерево из ненадежных данных. Оказывается, ожидаемая высота случайно построенного двоичного дерева поиска по-прежнему равна O (lg (n)), точнее, ожидается, что она будет не более 3 · lg (n).
Темы, объясненные в девятой лекции:
- Каковы хорошие и плохие деревья двоичного поиска?
- Сортировка дерева двоичного поиска.
- Анализ сортировки дерева двоичного поиска.
- отношение сортировки BST к быстрой сортировке.
- Рандомизированная сортировка BST.
- Случайно построенные деревья двоичного поиска.
- Выпуклые функции, неравенство Йенсена.
- Ожидаемая высота случайно построенного BST.
Самая удивительная идея в этой лекции заключается в том, что сортировка дерева двоичного поиска (представленная в этой лекции) выполняет те же сравнения элементов, что и быстрая сортировка, то есть они создают такое же дерево решений.
Перейдите по этой ссылке, чтобы увидеть полный обзор девятой лекции.
Лекция 10: Поисковые деревья (продолжение)
Это вторая лекция о деревьях поиска. В нем обсуждаются самобалансирующиеся деревья, а точнее красно-черные деревья. Они уравновешивают себя таким образом, что независимо от входа их высота всегда равна O (lg (n)).
Темы, объясненные в десятой лекции:
- Сбалансированные деревья поиска.
- Красно-черные деревья.
- Высота красно-черных деревьев.
- Вращения в бинарных деревьях.
- Как вставить элемент в красно-черное дерево?
- Алгоритм вставки элементов для красно-черных деревьев.
Перейдите по этой ссылке, чтобы увидеть полный обзор десятой лекции.
Лекция 11: Расширение структур данных
В одиннадцатой лекции объясняется, как построить новые структуры данных из существующих. Например, как построить структуру данных, которую можно быстро обновить и запросить i-й наименьший элемент.Это проблема динамической статистики порядка, и ее простое решение — дополнить двоичное дерево, например, красно-черное дерево. Другой пример — деревья интервалов — как быстро найти интервал (например, 5–9), который перекрывает некоторые другие интервалы (например, 4–11 и 8–20).
Темы, объясненные в одиннадцатой лекции:
- Динамическая статистика заказов.
- Расширение структуры данных.
- Интервальные деревья.
- Добавление красно-черных деревьев, чтобы они работали как интервальные деревья.
- Корректность структуры данных расширенного красно-черного дерева.
Дополнение структур данных требует большого творчества. Сначала вам нужно найти базовую структуру данных (самый простой шаг), а затем подумать о способе дополнить ее данными, чтобы заставить ее делать то, что вы хотите (самый сложный шаг).
Перейдите по этой ссылке, чтобы увидеть полный обзор одиннадцатой лекции.
Лекция 12: Пропускаемые списки
Эта лекция объясняет списки пропуска, которые представляют собой простую, эффективную, легко реализуемую рандомизированную структуру поиска.Он работает так же хорошо, как и сбалансированное двоичное дерево поиска, но его гораздо проще реализовать. Эрик Демейн говорит, что реализовал его за 40 минут до занятия (10 минут на реализацию и 30 минут на отладку).
В этой лекции Эрик строит эту структуру данных с нуля. Он начинает со связанного списка и создает пару связанных списков до трех связанных списков, пока не найдет оптимальное количество связанных списков, необходимое для достижения логарифмического времени поиска.
Далее он продолжает объяснять, как алгоритмически построить такую структуру, и доказывает, что поиск в этой структуре данных действительно быстрый.
Перейдите по этой ссылке, чтобы увидеть полный обзор двенадцатой лекции.
Лекция 13: Амортизированный анализ
Амортизированный анализ — это метод, показывающий, что даже если несколько операций в последовательности операций являются дорогостоящими, общая производительность остается хорошей. Хороший пример — добавление элементов в динамический список (например, список в Python). Каждый раз, когда список заполняется, Python должен выделять больше места, а это дорого. Амортизированный анализ можно использовать, чтобы показать, что средняя стоимость вставки по-прежнему составляет O (1), даже несмотря на то, что Python иногда приходится выделять больше места для списка.
Темы, объясненные в тринадцатой лекции:
- Насколько большой должна быть хеш-таблица?
- Динамические столы.
- Амортизированный анализ.
- Бухгалтерский метод амортизированного анализа.
- Динамический табличный анализ с бухгалтерским методом.
- Возможный метод амортизационного анализа.
- Анализ динамических таблиц с потенциальным методом.
Это одна из самых математически сложных лекций.
Перейдите по этой ссылке, чтобы увидеть полный обзор тринадцатой лекции.
Лекция 14: Самоорганизующиеся списки и анализ конкуренции
Эта лекция посвящена самоорганизующимся спискам. Самоорганизующийся список — это список, который переупорядочивается для уменьшения среднего времени доступа. Цель состоит в том, чтобы найти переупорядочение, которое минимизирует общее время доступа. Например, каждый раз, когда осуществляется доступ к элементу, он перемещается в начало списка, надеясь, что к нему вскоре снова можно будет получить доступ.Это называется эвристикой перехода на передний план.
Конкурентный анализ может быть использован для теоретического обоснования эффективности такой стратегии, как перемещение элементов на передний план.
Темы, объясненные в четырнадцатой лекции:
- Самоорганизующиеся списки.
- Онлайн и офлайн алгоритмы
- Анализ наихудшего случая самоорганизующихся списков.
- Конкурентный анализ.
- Эвристика перехода на передний план для самоорганизующихся списков.
- Амортизированная стоимость эвристики перехода на передний план.
Перейдите по этой ссылке, чтобы увидеть полный обзор четырнадцатой лекции.
Лекция 15: Динамическое программирование
Эта лекция посвящена технике разработки алгоритмов динамического программирования. Это табличный метод (включающий построение таблицы или некоторой части таблицы), который приводит к гораздо более быстрому времени выполнения алгоритма.
Лекция фокусируется на самой длинной общей проблеме подпоследовательности, сначала демонстрируется алгоритм грубой силы, затем рекурсивный и, наконец, алгоритм динамического программирования.Алгоритм грубой силы экспоненциально зависит от длины строк, рекурсивный алгоритм также является экспоненциальным, но решение динамического программирования — O (n · m), где n — длина одной строки, а m — длина другой.
Темы, объясненные в пятнадцатой лекции:
- Идея динамического программирования.
- Задача самой длинной общей подпоследовательности (LCS).
- Алгоритм грубой силы для LCS.
- Анализ алгоритма перебора.
- Упрощенный алгоритм LCS.
- Признак №1 динамического программирования: оптимальная подструктура.
- Признак № 2 динамического программирования: перекрывающиеся подзадачи.
- Рекурсивный алгоритм для LCS.
- Воспоминание.
- Алгоритм динамического программирования для LCS.
Самое интересное в этой лекции — это два признака, которые указывают на то, что проблема может быть решена с помощью динамического программирования. Это «оптимальная подструктура» и «перекрывающиеся подзадачи».
Первый означает, что оптимальное решение проблемы содержит оптимальное решение подзадач. Например, если z = LCS (x, y) — z является решением проблемы LCS (x, y), то любой префикс z является решением LCS префикса x и префикса y (префикс z это решение подзадач).
Второй означает именно то, что он говорит, что проблема содержит много перекрывающихся подзадач.
Перейдите по этой ссылке, чтобы увидеть полный обзор пятнадцатой лекции.
Лекция 16: Жадные алгоритмы
В этой лекции были представлены жадные алгоритмы с помощью задачи минимального охвата трех.Задача минимального остовного дерева состоит в том, чтобы найти дерево, которое соединяет все вершины графа с минимальным весом ребер. Сначала кажется, что решение динамического программирования могло бы решить эту проблему эффективно, но если проанализировать более внимательно, можно заметить, что проблема демонстрирует еще одно мощное свойство — лучшее решение каждой из подзадач приводит к глобально оптимальному решению. Поэтому это называется жадным, он всегда выбирает лучшее решение для подзадач, даже не задумываясь обо всей проблеме в целом.
Темы, объясненные в шестнадцатой лекции:
- Просмотр графиков.
- Графические представления.
- Матрицы смежности.
- Списки смежности.
- Редкие и плотные графы.
- Лемма о рукопожатии.
- Минимальные остовные деревья (MST).
- Отличительный признак жадных алгоритмов: свойство жадного выбора.
- Алгоритм Прима для поиска MST.
- Анализ времени работы алгоритма Прима.
- Идея алгоритма Крускала для MST.
Перейдите по этой ссылке, чтобы увидеть полный обзор шестнадцатой лекции.
Лекция 17: Алгоритмы кратчайшего пути
Эта лекция начинает трилогию об алгоритме кратчайшего пути. В этом первом эпизоде обсуждаются алгоритмы кратчайшего пути из одного источника. Проблему можно описать следующим образом — как добраться из одной точки на графике в другую, преодолев кратчайшее расстояние (подумайте о дорожной сети). Алгоритм Дейкстры эффективно решает эту проблему.
Темы, объясненные в семнадцатой лекции:
- Пути в графах.
- Кратчайшие пути.
- Вес пути.
- Отрицательные веса пути.
- Кратчайший путь от одного источника.
- Алгоритм Дейкстры.
- Пример алгоритма Дейкстры.
- Правильность алгоритма Дейкстры.
- Невзвешенные графики.
- Поиск в ширину.
Самое интересное здесь то, что алгоритм Дейкстры для невзвешенных графов сводится к алгоритму поиска в ширину, который использует FIFO вместо очереди с приоритетами, потому что больше нет необходимости отслеживать кратчайшее расстояние (все пути имеют тот же вес).
Перейдите по этой ссылке, чтобы увидеть полный обзор семнадцатой лекции.
Лекция 18: Алгоритмы кратчайшего пути (продолжение)
Вторая лекция трилогии о кратчайших путях посвящена кратчайшим путям с одним источником, которые могут иметь отрицательные веса ребер. Алгоритм Беллмана-Форда решает задачу поиска кратчайшего пути для графов с отрицательными ребрами.
Темы, объясненные в восемнадцатой лекции:
- Алгоритм Беллмана-Форда для кратчайших путей с отрицательными ребрами.
- Циклы отрицательного веса.
- Корректность алгоритма Беллмана-Форда.
- Линейное программирование.
- Линейная задача выполнимости.
- Различия ограничений.
- График ограничений.
- Использование алгоритма Беллмана-Форда для решения системы разностных ограничений.
- Решение проблемы компоновки СБИС (очень крупномасштабная интеграция) через Bellman-Ford.
Перейдите по этой ссылке, чтобы увидеть полный обзор восемнадцатой лекции.
Лекция 19: Алгоритмы кратчайшего пути (продолжение)
Последняя лекция трилогии посвящена задаче кратчайших путей для всех пар — определению кратчайших расстояний между каждой парой вершин в заданном графе.
Темы, объясненные в девятнадцатой лекции:
- Обзор проблемы кратчайшего пути из одного источника.
- Кратчайшие пути для всех пар.
- Динамическое программирование.
- Идея из матричного умножения.
- Алгоритм Флойда-Уоршалла для кратчайших путей для всех пар.
- Транзитивное замыкание ориентированного графа.
- Алгоритм Джонсона для кратчайших путей для всех пар.
Интересный момент заключается в том, как алгоритм Флойда-Уоршалла, который выполняется в O ((количество вершин) 3 ), может быть преобразован во что-то похожее на алгоритм Штрассена для вычисления транзитивного замыкания графа (теперь он работает в O ((количество вершин) lg7 ).
Перейдите по этой ссылке, чтобы увидеть полный обзор девятнадцатой лекции.
Лекция 20: Параллельные алгоритмы
Это вводная лекция по анализу многопоточных алгоритмов. В нем объясняется терминология, используемая в многопоточных алгоритмах, таких как работа, критическая длина пути, ускорение, параллелизм, планирование и другие.
Темы, объясненные в лекции двадцать:
- Динамическая многопоточность.
- Подпрограммы: создание и синхронизация.
- Логический параллелизм и фактический параллелизм.
- Многопоточные вычисления.
- Пример многопоточного выполнения рекурсивного алгоритма Фибоначчи.
- Измерение производительности многопоточных вычислений.
- Понятие об ускорении.
- Максимально возможное ускорение.
- Линейное ускорение.
- Суперлинейное ускорение.
- Параллельность.
- Планирование.
- Жадный планировщик.
- Теорема Гранд и Брента о конкурентоспособности жадных графиков.
- * Шахматные программы Сократа и Силкчесса.
Перейдите по этой ссылке, чтобы увидеть полный обзор лекции двадцать.
Лекция 21: Параллельные алгоритмы (продолжение)
Вторая лекция о параллельных алгоритмах показывает, как проектировать и анализировать многопоточный алгоритм умножения матриц и многопоточную сортировку.
Темы, объясненные в двадцать первой лекции:
- Многопоточные алгоритмы.
- Многопоточное матричное умножение.
- Анализ производительности многопоточного алгоритма умножения матриц.
- Многопоточная сортировка.
- Многопоточный алгоритм сортировки слиянием.
- Подпрограмма параллельного слияния.
- Анализ сортировки слиянием с помощью подпрограммы параллельного слияния.
Перейдите по этой ссылке, чтобы получить полный обзор лекции двадцать один.
Лекция 22: Алгоритмы игнорирования кеширования
Алгоритмы без учета кэша учитывают то, что до сих пор игнорировалось во всех алгоритмах, в частности, кэш.Алгоритм, который можно преобразовать в эффективное использование кеша, будет работать намного лучше, чем тот, который этого не делает. Эта лекция посвящена тому, как расположить структуры данных в памяти таким образом, чтобы передачи памяти были минимальными.
Темы, объясненные в лекции двадцать второй:
- Современная иерархия памяти.
- Понятие пространственной локальности и временной локальности.
- Двухуровневая модель памяти.
- Алгоритмы без кеширования.
- Блокировка памяти.
- Передача памяти с помощью простого алгоритма сканирования.
- Передача памяти с использованием алгоритма обратного преобразования строки.
- Анализ памяти двоичного поиска.
- Кэшировать статистику незаметных заказов.
- Кэш-память алгоритма умножения матриц.
Перейдите по этой ссылке, чтобы увидеть полный обзор двадцать второй лекции.
Лекция 23: Алгоритмы забывающего кеширования (продолжение)
Это последняя лекция курса.Он продолжает алгоритмы, не обращающие внимания на кэш, и показывает, как хранить двоичные деревья поиска в памяти, чтобы минимизировать передачу памяти при поиске в них. Он завершается сортировкой кеша без внимания.
Темы, объясненные в двадцать третьей лекции:
- Статические деревья поиска.
- Разметка статических двоичных деревьев поиска в памяти с эффективным использованием памяти.
- Анализ статических деревьев поиска.
- Сортировка с учетом кеша.
- Сортировка без кеширования.
- Воронка сортировки.
- Структура данных K-воронки.
Это самая сложная лекция за весь курс. На понимание структуры данных k-воронки уходит день.
Перейдите по этой ссылке, чтобы увидеть полный обзор двадцать третьей лекции.
Вот и все. Это была последняя лекция. Надеюсь, вы найдете это резюме полезным.
Что дальше?
Затем я отправлю свои заметки по курсу линейной алгебры Массачусетского технологического института. Сначала я подумал, что выложу линейную алгебру в отдельный раздел блога, которого нет в RSS-потоке, но потом я подумал еще раз и пришел к выводу, что каждый компетентный программист должен знать линейную алгебру и поэтому стоит их поместить в ленте.Вы, безусловно, можете быть хорошим программистом, не зная линейной алгебры, но если вы хотите работать над большими проблемами и что-то изменить, вам обязательно нужно это знать.
Оставайтесь с нами!
Обновление
: Вышел обзор первой лекции — Лекции 1: Геометрия линейных уравнений.
Введение в разработку алгоритмов | SpringerLink
- Стивен С. Скиена
Глава
1
Цитаты- 221 тыс.
Загрузки
Аннотация
Что такое алгоритм? Алгоритм — это процедура для выполнения определенной задачи.Алгоритм — это идея любой разумной компьютерной программы.
Чтобы быть интересным, алгоритм должен решать общую, хорошо специфицированную задачу . Алгоритмическая проблема определяется описанием полного набора из экземпляров , над которыми он должен работать, и его выходных данных после запуска в одном из этих экземпляров. Это различие между проблемой и экземпляром проблемы является фундаментальным.
Ключевые слова
Разработка алгоритма Задача коммивояжера Задача коммивояжера Формула суммирования Входной экземпляр
Эти ключевые слова были добавлены машиной, а не авторами.Это экспериментальный процесс, и ключевые слова могут обновляться по мере улучшения алгоритма обучения.
Это предварительный просмотр содержимого подписки,
войдите в
, чтобы проверить доступ.
Предварительный просмотр
Невозможно отобразить предварительный просмотр. Скачать превью PDF.
Библиография
[Bro95]
F. Brooks.
Мифический человеко-месяц
. Эддисон-Уэсли, Ридинг, Массачусетс, выпуск к 20-летию, 1995.
Google Scholar
[CLRS01]
T.Кормен, К. Лейзерсон, Р. Ривест и К. Стейн.
Введение в алгоритмы
. MIT Press, Cambridge MA, второе издание, 2001.
zbMATHGoogle Scholar
[Gol04]
M. Golumbic.
Алгоритмическая теория графов и совершенные графы
, том 57 из
Анналы дискретной математики
. Северная Голландия, второе издание, 2004 г.
Google Scholar
[Gri89]
Д. Грис.
Наука программирования
.Springer-Verlag, 1989.
Google Scholar
[KT06]
Дж. Кляйнберг и Э. Тардос.
Разработка алгоритмов
. Addison Wesley, 2006.
Google Scholar
[Man89]
У. Манбер.
Введение в алгоритмы
. Addison-Wesley, Reading MA, 1989.
zbMATHGoogle Scholar
[Raw92]
G. Rawlins.
По сравнению с чем?
Computer Science Press, Нью-Йорк, 1992.
Google Scholar
[YS96]
Ф. Юнас и С. Скиена. Рандомизированные алгоритмы определения минимальных наборов лотерейных билетов.
Journal of Undergraduate Research
, 2-2: 88–97, 1996.
Google Scholar
Информация об авторских правах
© Springer-Verlag London Limited 2012
Авторы и филиалы
- 1.Департамент информатики государства Университет Нью-Йорка в Стоуни-Брук, штат Нью-Йорк, США,
Введение в алгоритмы.Что такое алгоритм? Основы алгоритмов | by Tusamma Sal Sabil
Слово Алгоритм означает «процесс или набор правил, которым необходимо следовать при вычислениях или других операциях по решению проблем». Следовательно, алгоритм относится к набору правил / инструкций, которые шаг за шагом определяют, как должна выполняться работа, чтобы получить ожидаемые результаты.
Это можно понять на примере приготовления нового рецепта. Чтобы приготовить новый рецепт, нужно прочитать инструкции и шаги и выполнить их один за другим в заданной последовательности.В результате получается новое блюдо, приготовленное безупречно. Точно так же алгоритмы помогают выполнить задачу в программировании, чтобы получить ожидаемый результат.
Разработанный алгоритм не зависит от языка, то есть это просто простые инструкции, которые могут быть реализованы на любом языке, и все же результат будет таким же, как и ожидалось.
Поскольку при приготовлении рецепта нельзя следовать никаким письменным инструкциям, а только стандартным. Точно так же не все письменные инструкции по программированию представляют собой алгоритм.Чтобы некоторые инструкции были алгоритмом, он должен иметь следующие характеристики:
- Четкий и недвусмысленный : Алгоритм должен быть четким и однозначным. Каждый его шаг должен быть ясным во всех аспектах и иметь только одно значение.
- Хорошо определенные входы : Если алгоритм говорит принимать входные данные, это должны быть четко определенные входные данные.
- Хорошо определенные выходные данные: Алгоритм должен четко определять, какой результат будет получен, и он также должен быть четко определен.
- Конечность: Алгоритм должен быть конечным, то есть он не должен заканчиваться бесконечными циклами или чем-то подобным.
- Выполнимо: Алгоритм должен быть простым, универсальным и практичным, чтобы его можно было выполнять при наличии доступных ресурсов. Он не должен содержать какие-то технологии будущего или что-то еще.
- Независимость от языка: Разработанный алгоритм должен быть независимым от языка, то есть это должны быть простые инструкции, которые могут быть реализованы на любом языке, и все же результат будет таким же, как и ожидалось.
Для написания алгоритма необходимы следующие условия в качестве предварительных условий:
- Задача , которая должна быть решена этим алгоритмом.
- ограничивает задачи, которые необходимо учитывать при решении задачи.
- Вход , который нужно использовать для решения проблемы.
- Выход следует ожидать, когда проблема будет решена.
- Решение этой задачи в заданных ограничениях.
Нет, алгоритмы связаны не только с информатикой, но в нашем мире это компьютер, который обрабатывает и обрабатывает очень большие объемы данных. Даже если говорить о областях, не относящихся к информатике, алгоритмы — это просто четко определенные шаги для решения проблемы, а разработка алгоритма — это работа мозга, поэтому здесь не требуется никакого кодирования. Мы разрабатываем алгоритмы для расчета положения манипулятора или траектории движения жидкости, и это не только области компьютерных наук.И эти алгоритмы довольно успешно дают результат, если размер проблемы небольшой.
Большая часть наших реальных проблем связана не с десятками или сотнями данных, а с гораздо большим числом, например, с тысячами и миллионами. Таким образом, выполнение этих шагов в наборах данных, которые намного больше, не является задачей человека, и нам нужно разработать код для реализации этих шагов на компьютере. Даже компьютеру потребуется значительное количество времени (например, дни, недели или даже больше), если алгоритм, который мы разработали, не очень хорош, и тогда нам нужно оптимизировать наш алгоритм.Итак, разработка эффективного алгоритма очень важна для решения многих практических задач.
Предположим, вы обедаете в своем любимом ресторане, и вам очень понравилась еда, и вы хотите приготовить ее самостоятельно, но никогда раньше ничего не готовили. Даже если вы никогда ничего не готовили, но все же знаете, как готовится еда, но достаточно ли этих знаний, чтобы приготовить еду, которую вы ели в ресторане? Возможно, нет. Но что, если вы хорошо разбираетесь в кулинарии и знаете, как приготовить еду с определенным вкусом, текстурой и т. Д., можете ли вы создать рецепт, соответствующий вкусу, который вы пробовали? Возможно — да.
Дело в том, что если у вас есть предварительные знания о решении проблем (приготовление еды в этом примере), то вы можете решить более сложную задачу самостоятельно (в данном случае приготовление еды, подаваемой в ресторане). И любой курс по алгоритмам заставляет вас сначала столкнуться с некоторыми проблемами, так что вы будете готовы решать дальнейшие гораздо более сложные проблемы самостоятельно или создать алгоритм для решения совершенно новой проблемы.
Итак, это реальный вопрос, по крайней мере, если вы новичок, вы так думаете. Кроме того, время — это не единственное, что нас беспокоит, мы также оптимизируем наш алгоритм, чтобы он занимал меньше места (памяти), усилий программиста и т. Д. Во многих случаях. Ответ на эти вопросы в одну строку: нам не предоставляется компьютер с неограниченной скоростью и пространством, поэтому нам необходимо оптимизировать наш подход для решения проблемы с помощью компьютера.
Даже при наличии на рынке высокопроизводительных компьютеров плохо написанный алгоритм может занять значительное количество времени, например, дни, недели или даже больше.Однако оптимизированный алгоритм может выполнить ту же работу за минуты или секунды на гораздо более медленном компьютере.
Просто попробуйте запустить этот код, чтобы напечатать первые 10 000 простых чисел, и обратите внимание, сколько времени требуется, чтобы получить все результаты.
def is_prime (x):
prime = True
для i в диапазоне (2, x):
if x% i == 0:
prime = False
return primeif __name__ == '__main__':
count = 0 ;
число = 2;
while (count <10000):
if (is_prime (number)):
print (number)
count = count + 1
number = number + 1
Купить Введение в алгоритмы (издание для Восточной экономики) Забронировать онлайн по низким ценам в Индии | Введение в алгоритмы (издание для Восточной экономики) Обзоры и рейтинги
«Как педагог и исследователь в области алгоритмов на протяжении более двух десятилетий, я могу однозначно сказать, что книга Кормена и др. — лучший учебник, который я когда-либо видел по этой теме.Он предлагает проницательный, энциклопедический и современный подход к алгоритмам, и наш отдел будет продолжать использовать его для обучения как на уровне магистратуры, так и на уровне бакалавриата, а также в качестве надежного справочного материала для исследований ».
— Габриэль Робинс, Департамент компьютерных наук. , Университет Вирджинии
«Введение в алгоритмы,« библия »в этой области, представляет собой исчерпывающий учебник, охватывающий весь спектр современных алгоритмов: от самых быстрых алгоритмов и структур данных до алгоритмов с полиномиальным временем для кажущихся неразрешимыми проблем, от классических от алгоритмов теории графов до специальных алгоритмов сопоставления строк, вычислительной геометрии и теории чисел.В пересмотренное третье издание примечательно добавлена глава о деревьях Ван Эмде Боаса, одной из наиболее полезных структур данных, и о многопоточных алгоритмах, тема, которая приобретает все большее значение. «
— Дэниел Спилман, факультет компьютерных наук, Йельский университет
» В свете стремительного роста объема данных и разнообразия вычислительных приложений эффективные алгоритмы необходимы сейчас как никогда. Эта красиво написанная, тщательно организованная книга является исчерпывающим вводным пособием по проектированию и анализу алгоритмов.Первая половина предлагает эффективный метод обучения и изучения алгоритмов; вторая половина затем привлекает более продвинутых читателей и любопытных студентов с убедительным материалом как о возможностях, так и о проблемах в этой увлекательной области ».
— Шан-Хуа Тенг, Университет Южной Калифорнии
Томас Х. Кормен получил степень бакалавра электротехники в Принстонском университете еще в 1978 году. После этого он получил степень магистра электротехники и информатики в Массачусетском технологическом институте.Среди студентов он наиболее известен как соавтор книги под названием «Введение в алгоритмы». В 2013 году он опубликовал еще одну книгу под названием «Разблокированные алгоритмы». Эта книга тоже была принята хорошо.
Чарльз Э. Лейзерсон — профессор компьютерных наук и инженерии Массачусетского технологического института. Рональд Л. Ривест — профессор электротехники и компьютерных наук Эндрю и Эрны Витерби в Массачусетском технологическом институте. Клиффорд Штайн — профессор промышленной инженерии и операционных исследований Колумбийского университета.
Введение в структуры данных и алгоритмы
Структура данных
— это способ сбора и организации данных таким образом, чтобы мы могли эффективно выполнять операции с этими данными. Структуры данных — это визуализация элементов данных с точки зрения некоторой взаимосвязи для лучшей организации и хранения. Например, у нас есть некоторые данные, которые содержат: имя игрока «Virat» и возраст 26. Здесь «Virat» имеет тип данных String, , а 26 — тип данных целое число .
Мы можем организовать эти данные в виде записи, например, Player record, в которой будут указаны как имя игрока, так и возраст. Теперь мы можем собирать и хранить записи игроков в файле или базе данных в виде структуры данных.
Например: : «Дони» 30, «Гамбхир» 31, «Сехваг» 33
Если вы знакомы с концепциями объектно-ориентированного программирования, то класс также делает то же самое: он собирает данные разных типов в рамках одного объекта. Единственная разница в том, что структуры данных предоставляют методы для эффективного доступа к данным и управления ими.
Проще говоря, структуры данных — это структуры, запрограммированные для хранения упорядоченных данных, чтобы с ними можно было легко выполнять различные операции. Он представляет собой знание данных, которые необходимо организовать в памяти. Он должен быть спроектирован и реализован таким образом, чтобы упростить его и повысить эффективность.
Основные типы структур данных
Как мы обсуждали выше, все, что может хранить данные, может называться структурой данных, следовательно, Integer, Float, Boolean, Char и т. Д. — все это структуры данных.Они известны как примитивные структуры данных .
Кроме того, у нас есть несколько сложных структур данных, которые используются для хранения больших и связанных данных. Некоторые примеры абстрактной структуры данных :
Все эти структуры данных позволяют нам выполнять различные операции с данными. Мы выбираем эти структуры данных в зависимости от того, какой тип операции требуется. Мы рассмотрим эти структуры данных более подробно в наших последующих уроках.
Структуры данных также можно классифицировать на основе следующих характеристик:
| Характерный | Описание |
|---|---|
| Линейный | В линейных структурах данных элементы данных расположены в линейной последовательности.Пример: Массив |
| Нелинейный | В нелинейных структурах данных элементы данных расположены не по порядку. Пример: Дерево , График |
| Однородный | В однородных структурах данных все элементы одного типа. Пример: Массив |
| Неоднородный | В неоднородной структуре данных элементы могут быть одного типа, а могут и не быть. Пример: Структуры |
| Статические | Статические структуры данных — это те структуры, чьи размеры и связанные ячейки памяти фиксированы во время компиляции.Пример: Массив |
| Динамический | Динамические структуры — это те структуры, которые расширяются или сжимаются в зависимости от потребности программы и ее выполнения. Кроме того, меняются связанные с ними ячейки памяти. Пример: Связанный список, созданный с использованием указателей |
Что такое алгоритм?
Алгоритм — это конечный набор инструкций или логики, написанных по порядку для выполнения определенной заранее определенной задачи. Алгоритм — это не полный код или программа, это просто основная логика (решение) проблемы, которая может быть выражена либо как неформальное описание высокого уровня как псевдокод , либо с использованием блок-схемы .
Каждый алгоритм должен удовлетворять следующим свойствам:
- Входные данные — Для внешнего алгоритма должно быть 0 или более входов.
- Выходные данные — Должен быть получен как минимум 1 выходной.
- Определенность — Каждый шаг алгоритма должен быть четким и четко определенным.
- Finiteness — Алгоритм должен иметь конечное количество шагов.
- Корректность — Каждый шаг алгоритма должен генерировать правильный результат.
Алгоритм считается эффективным и быстрым, если он занимает меньше времени и занимает меньше места в памяти. Производительность алгоритма измеряется на основе следующих свойств:
- Сложность времени
- Космическая сложность
Сложность пространства
Это объем памяти, необходимый алгоритму в процессе его выполнения. Сложность пространства следует воспринимать серьезно для многопользовательских систем и в ситуациях, когда доступная память ограничена.
Алгоритм обычно требует места для следующих компонентов:
- Пространство для инструкций: Это пространство, необходимое для хранения исполняемой версии программы. Это пространство фиксировано, но зависит от количества строк кода в программе.
- Data Space: Это пространство, необходимое для хранения всех значений констант и переменных (включая временные переменные).
- Environment Space: Это пространство, необходимое для хранения информации о среде, необходимой для возобновления приостановленной функции.
Чтобы подробнее узнать о космической сложности, перейдите к учебнику «Космическая сложность».
Сложность времени
Сложность времени — это способ представить количество времени, необходимое программе для выполнения до ее завершения. Как правило, рекомендуется стараться сохранять необходимое время минимальным, чтобы наш алгоритм завершил свое выполнение за минимально возможное время.


 2012; 4: 111-115.]
2012; 4: 111-115.]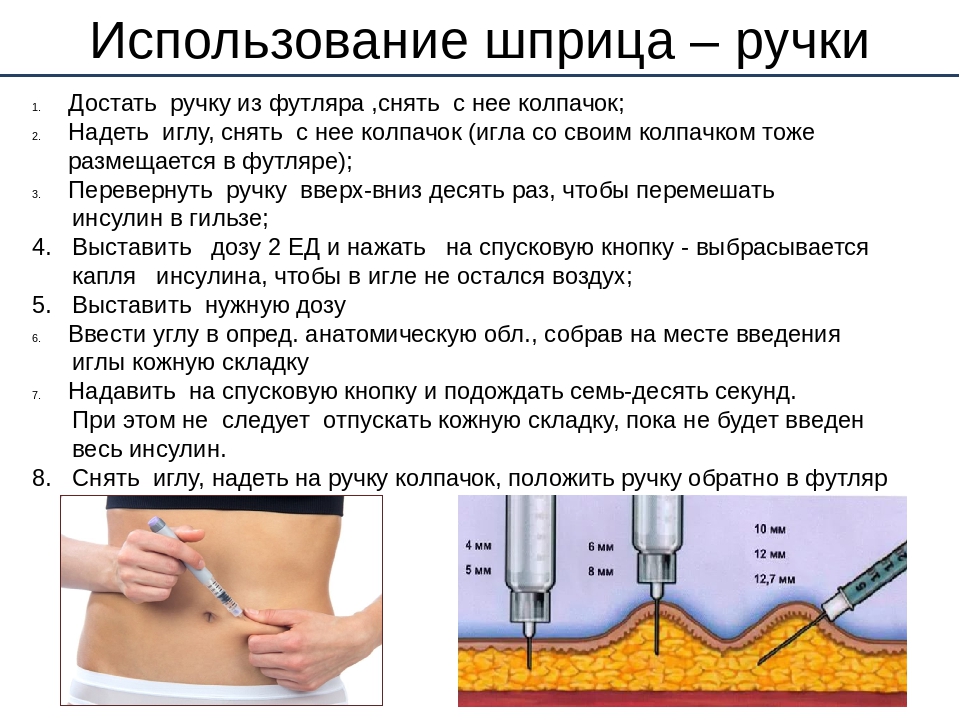 Poster presented at ESPGHAN, Geneva, Switzerland, 2018.
Poster presented at ESPGHAN, Geneva, Switzerland, 2018.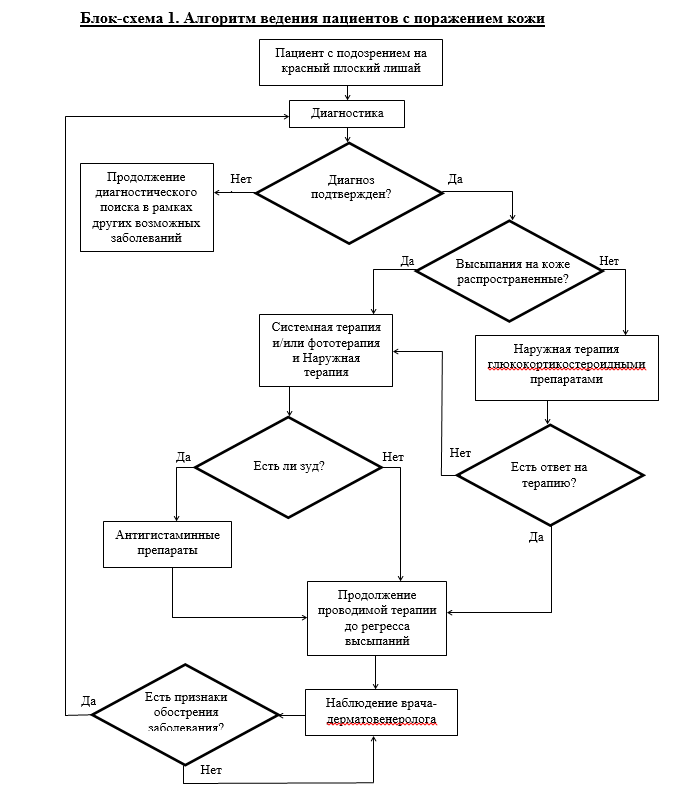 2017; 3 (16).]
2017; 3 (16).]